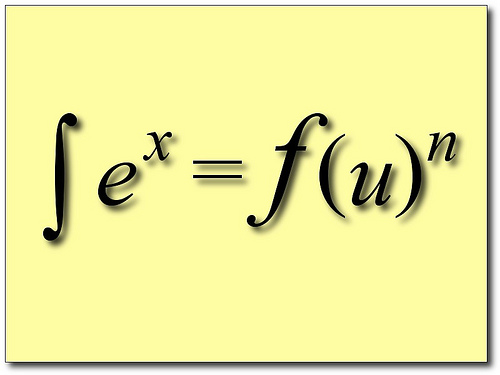The last couple of months in finance industry can be summarized in two words — chaos and uncertainty. The aptness of this laconic description is all too evident. The sub-prime crisis where everybody lost, the dizzying commodity price movements, the pink slip syndrome, the spectacular bank busts and the gargantuan bail-outs all vouch for it.
The financial meltdown is such a rich topic with reasons and ramifications so overarching that all self-respecting columnists will be remiss to let it slide. After all, a columnist who keeps his opinions to himself is a columnist only in his imagination. I too will share my views on causes and effects of this turmoil that is sure to affect our lives more directly than anybody else’s, but perhaps in a future column.
The chaos and uncertainty I want to talk about are of different kind — the physics kind. The terms chaos and uncertainty have a different and specific meanings in physics. How those meanings apply to the world of finance is what this column is about.
Symmetries and Patterns
Physicists are a strange bunch. They seek and find symmetries and patterns where none exists. I remember once when our brilliant professor, Lee Smolin, described to us how the Earth could be considered a living organism. Using insightful arguments and precisely modulated articulation, Lee made a compelling case that the Earth, in fact, satisfied all the conditions of being an organism. The point in Lee’s view was not so much whether or the Earth was literally alive, but that thinking of it as an organism was a viable intellectual pattern. Once we represent the Earth in that model, we can use the patterns pertaining to organism to draw further predictions or conclusions.
Expanding on this pattern, I recently published a column presenting the global warming as a bout of fever caused by a virus (us humans) on this host organism. Don’t we plunder the raw material of our planet with the same abandon with which a virus usurps the genetic material of its host? In addition to fever, typical viral symptoms include sores and blisters as well. Looking at the cities and other eye sores that have replaced pristine forests and other natural landscapes, it is not hard to imagine that we are indeed inflicting fetid atrocities to our host Earth. Can’t we think of our city sewers and the polluted air as the stinking, oozing ulcers on its body?
While these analogies may sound farfetched, we have imported equally distant ideas from physics to mathematical finance. Why would stock prices behave anything like a random walk, unless we want to take Bush’s words (that “Wall Street got drunk”) literally? But seriously, Brownian motion has been a wildly successful model that we borrowed from physics. Again, once we accept that the pattern is similar between molecules getting bumped around and the equity price movements, the formidable mathematical machinery and physical intuitions available in one phenomenon can be brought to bear on the other.
Looking at the chaotic financial landscape now, I wonder if physics has other insights to offer so that we can duck and dodge as needed in the future. Of the many principles from physics, chaos seems such a natural concept to apply to the current situation. Are there lessons to be learned from chaos and nonlinear dynamics that we can make use of? May be it is Heisenberg’s uncertainty principle that holds new insights.
Perhaps I chose these concepts as a linguistic or emotional response to the baffling problems confronting us now, but let’s look at them any way. It is not like the powers that be have anything better to offer, is it?
Chaos Everywhere
In physics, chaos is generally described as our inability to predict the outcome of experiments with arbitrarily close initial conditions. For instance, try balancing your pencil on its tip. Clearly, you won’t be able to, and the pencil will land on your desktop. Now, note this line along which it falls, and repeat the experiment. Regardless of how closely you match the initial conditions (of how you hold and balance the pencil), the outcome (the line along which it falls) is pretty much random. Although this randomness may look natural to us — after all, we have been trying to balance pencils on their tips ever since we were four, if my son’s endeavours are anything to go by — it is indeed strange that we cannot bring the initial conditions close enough to be confident of the outcome.
Even stranger is the fact that similar randomness shows up in systems that are not quite as physical as pencils or experiments. Take, for instance, the socio-economic phenomenon of globalization, which I can describe as follows, admittedly with an incredible amount of over-simplification. Long time ago, we used to barter agricultural and dairy products with our neighbours — say, a few eggs for a litre (or was it pint?) of milk. Our self-interest ensured a certain level of honesty. We didn’t want to get beaten up for adding white paint to milk, for instance. These days, thanks to globalization, people don’t see their customers. A company buys milk from a farmer, adds god knows what, makes powder and other assorted chemicals in automated factories and ships them to New Zealand and Peru. The absence of a human face in the supply chain and in the flow of money results in increasingly unscrupulous behaviour.
Increasing chaos can be seen in the form of violently fluctuating concentrations of wealth and fortunes, increasing amplitudes and frequency of boom and bust cycles, exponential explosion in technological innovation and adaptation cycles, and the accelerated pace of paradigm shifts across all aspects of our lives.
It is one thing to say that things are getting chaotic, quite another matter to exploit that insight and do anything useful with it. I won’t pretend that I can predict the future even if (rather, especially if) I could. However, let me show you a possible approach using chaos.
One of the classic examples of chaos is the transition from a regular, laminar flow of a fluid to a chaotic, turbulent flow. For instance, when you open a faucet slowly, if you do it carefully, you can have a pretty nice continuous column of water, thicker near the top and stretched thinner near the bottom. The stretching force is gravity, and the cohesive forces are surface tension and inter-molecular forces. As you open the faucet still further, ripples begin to appear on the surface of the column which, at higher rates of flow, rip apart the column into complete chaos.
In a laminar flow, macroscopic forces tend to smooth out microscopic irregularities. Like gravity and surface tension in our faucet example, we have analogues of macroscopic forces in finance. The stretching force is probably greed, and the cohesive ones are efficient markets.
There is a rich mathematical framework available to describe chaos. Using this framework, I suspect one can predict the incidence and intensity of financial turmoils, though not their nature and causes. However, I am not sure such a prediction is useful. Imagine if I wrote two years ago that in 2008, there would be a financial crisis resulting in about one trillion dollar of losses. Even if people believed me, would it have helped?
Usefulness is one thing, but physicists and mathematicians derive pleasure also from useless titbits of knowledge. What is interesting about the faucet-flow example is this: if you follow the progress two water molecules starting off their careers pretty close to each other, in the laminar case, you will find that they end up pretty much next to each other. But once the flow turns turbulent, there is not telling where the molecules will end up. Similarly, in finance, suppose two banks start off roughly from the same position — say Bear Stearns and Lehman. Under normal, laminar conditions, their stock prices would track similar patterns. But during a financial turbulence, they end up in totally different recycle bins of history, as we have seen.
If whole financial institutions are tossed around into uncertain paths during chaotic times, imagine where two roughly similar employees might end up. In other words, don’t feel bad if you get a pink slip. There are forces well beyond your control at play here.
Uncertainty Principle in Quantitative Finance
The Heisenberg uncertainty principle is perhaps the second most popular theme from physics that has captured the public imagination. (The first one, of course, is Einstein’s E = mc2.) It says something seemingly straightforward — you can measure two complementary properties of a system only to a certain precision. For instance, if you try to figure out where an electron is (measure its position, that is) more and more precisely, its speed becomes progressively more uncertain (or, the momentum measurement becomes imprecise).
Quantitative finance has a natural counterpart to the uncertainty principle — risks and rewards. When you try to minimize the risks, the rewards themselves go down. If you hedge out all risks, you get only risk-free returns. Since risk is the same as the uncertainty in rewards, the risk-reward relation is not quite the same as the uncertainty principle (which, as described in the box, deals with complementary variables), but it is close enough to draw some parallels.
To link the quantum uncertainty principle to quantitative finance, let’s look at its interpretation as observation altering results. Does modelling affect how much money we can make out of a product? This is a trick question. The answer might look obvious at first glance. Of course, if we can understand and model a product perfectly, we can price it right and expect to reap healthy rewards. So, sure, modelling affects the risk-reward equation.
But, a model is only as good as its assumptions. And the most basic assumption in any model is that the market is efficient and liquid. The validity of this assumption (or lack thereof) is precisely what precipitated the current financial crisis. If our modelling effort actually changes the underlying assumptions (usually in terms of liquidity or market efficiency), we have to pay close attention to the quant equivalent of the uncertainty principle.
Look at it this way — a pyramid scheme is a perfectly valid money making model, but based on one unfortunate assumption on the infinite number of idiots at the bottom of the pyramid. (Coming to think of it, the underlying assumption in the sub-prime crisis, though more sophisticated, may not have been that different.) Similar pyramid assumptions can be seen in social security schemes, as well. We know that pyramid assumptions are incorrect. But at what point do they become incorrect enough for us to change the model?
There is an even more insidious assumption in using models — that we are the only ones who use them. In order to make a killing in a market, we always have to know a bit more than the rest of them. Once everybody starts using the same model, I think the returns will plummet to risk-free levels. Why else do you think we keep inventing more and more complex exotics?
Summing up…
The current financial crisis has been blamed on many things. One favourite theory has been that it was brought about by the greed in Wall Street — the so-called privatization of profits and socialization of losses. Incentive schemes skewed in such a way as to encourage risk taking and limit risk management must take at least part of the blame. A more tempered view regards the turmoil as a result of a risk management failure or a regulatory failure.
This column presents my personal view that the turmoil is the inevitable consequence of the interplay between opposing forces in financial markets — risk and rewards, speculation and regulation, risk taking and risk management and so on. To the extent that the risk appetite of a financial institute is implemented through a conflict between such opposing forces, these crises cannot be avoided. Worse, the intensity and frequency of similar meltdowns are going to increase as the volume of transactions increases. This is the inescapable conclusion from non-linear dynamics. After all, such turbulence has always existed in the real economy in the form cyclical booms and busts. In free market economies, selfishness and the inherent conflicts between selfish interests provide the stretching and cohesive forces, setting the stage for chaotic turbulence.
Physics has always been a source of talent and ideas for quantitative finance, much like mathematics provides a rich toolkit to physics. In his book, Dreams of a Final Theory, Nobel Prize winning physicist Steven Weinberg marvels at the uncanny ability of mathematics to anticipate physics needs. Similarly, quants may marvel at the ability of physics to come up with phenomena and principles that can be directly applied to our field. To me, it looks like the repertoire of physics holds a few more gems that we can employ and exploit.
Box: Heisenberg’s Uncertainty PrincipleWhere does this famous principle come from? It is considered a question beyond the realms of physics. Before we can ask the question, we have to examine what the principle really says. Here are a few possible interpretations:
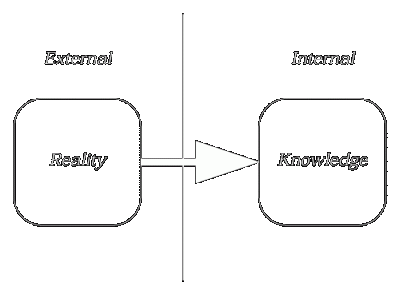
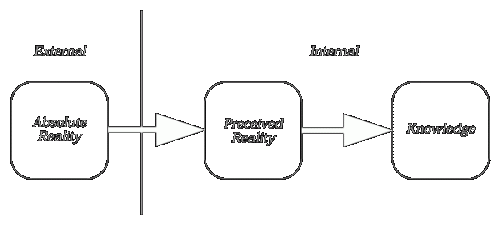
The first view is currently popular and is related to the so-called Copenhagen interpretation of quantum mechanics. Let’s ignore it for it is not too open to discussions. The second interpretation is generally understood as an experimental difficulty. But if the notion of the experimental setup is expanded to include the inevitable human observer, we arrive at the third view of perceptual limitation. In this view, it is actually possible to “derive” the uncertainty principle, based on how human perception works. Let’s assume that we are using a beam of light of wavelength 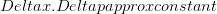 We can make this argument more rigorous, and get an estimate of the value of the constant. The resolution of a microscope is given by the empirical formula Through more rigorous statistical arguments, related to the spatial resolution and the expected momentum transferred, it may possible to derive the Heisenberg uncertainty principle through this line of reasoning. If we consider the philosophical view that our reality is a cognitive model of our perceptual stimuli (which is the only view that makes sense to me), my fourth interpretation of the uncertainty principle being a cognitive limitation also holds a bit of water. |
| About the Author The author is a scientist from the European Organization for Nuclear Research (CERN), who currently works as a senior quantitative professional at Standard Chartered in Singapore. More information about the author can be found at his blog: http//www.Thulasidas.com. The views expressed in this column are only his personal views, which have not been influenced by considerations of the firm’s business or client relationships. |

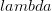 to observe the particle. The precision in the position we can hope to achieve is of the order of
to observe the particle. The precision in the position we can hope to achieve is of the order of 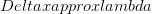 . In quantum mechanics, the momentum of each photon in the light beam is inversely proportional to the wavelength. At least one photon is reflected by the particle so that we can see it. So, by the classical conservation law, the momentum of the particle has to change by at least this amount(
. In quantum mechanics, the momentum of each photon in the light beam is inversely proportional to the wavelength. At least one photon is reflected by the particle so that we can see it. So, by the classical conservation law, the momentum of the particle has to change by at least this amount(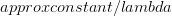 ) from what it was before the measurement. Thus, through perceptual arguments, we get something similar to the Heisenberg uncertainty principle
) from what it was before the measurement. Thus, through perceptual arguments, we get something similar to the Heisenberg uncertainty principle 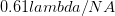 , where
, where 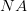 is the numerical aperture, which has a maximum value of one. Thus, the best spatial resolution is
is the numerical aperture, which has a maximum value of one. Thus, the best spatial resolution is 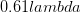 . Each photon in the light beam has a momentum
. Each photon in the light beam has a momentum 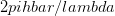 , which is the uncertainty in the particle momentum. So we get
, which is the uncertainty in the particle momentum. So we get 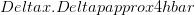 , approximately an order of magnitude bigger than the quantum mechanical limit.
, approximately an order of magnitude bigger than the quantum mechanical limit.
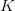 is moving with respect to another system
is moving with respect to another system 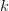 along the positive X axis of
along the positive X axis of  is receding while another object at a negative
is receding while another object at a negative 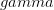 ray bursts and symmetric jets. As we showed in the article, perception of superluminal motion also holds an explanation for cosmological phenomena like the expansion of the universe and cosmic microwave background radiation. LTT effects should be considered as a fundamental constraint in our perception, and consequently in physics, rather than as a convenient explanation for isolated phenomena.
ray bursts and symmetric jets. As we showed in the article, perception of superluminal motion also holds an explanation for cosmological phenomena like the expansion of the universe and cosmic microwave background radiation. LTT effects should be considered as a fundamental constraint in our perception, and consequently in physics, rather than as a convenient explanation for isolated phenomena.
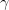 rays in the sky, lasting from a few milliseconds to several minutes, and are currently believed to emanate from cataclysmic stellar collapses. The short flashes (the prompt emissions) are followed by an afterglow of progressively softer energies. Thus, the initial
rays in the sky, lasting from a few milliseconds to several minutes, and are currently believed to emanate from cataclysmic stellar collapses. The short flashes (the prompt emissions) are followed by an afterglow of progressively softer energies. Thus, the initial 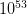 —
—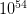 ergs in a few seconds. This energy output is similar to about 1000 times the total energy released by the sun over its entire lifetime.
ergs in a few seconds. This energy output is similar to about 1000 times the total energy released by the sun over its entire lifetime.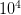 —
—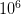 per day. Because of this inverse relationship between the rate and the estimated energy output, the total energy released per observed GRB remains the same.
per day. Because of this inverse relationship between the rate and the estimated energy output, the total energy released per observed GRB remains the same.
 to
to  through
through  and
and 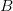 at a constant supersonic speed. Imagine that the object emits sound during its travel. The sound emitted at the point
at a constant supersonic speed. Imagine that the object emits sound during its travel. The sound emitted at the point 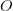 before the sound emitted earlier at
before the sound emitted earlier at 


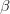 , and speed typically appears as
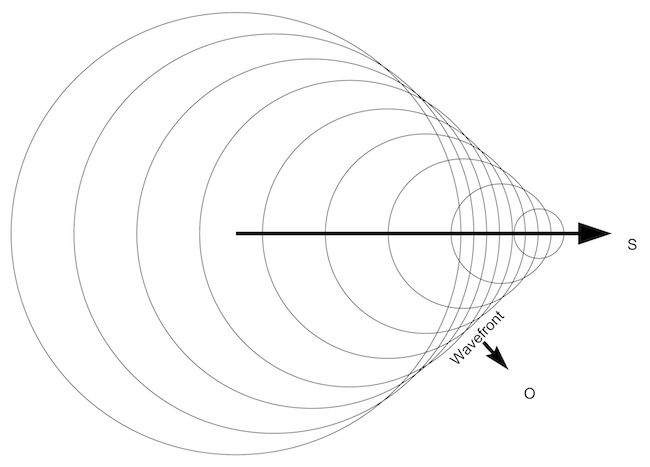
, and speed typically appears as 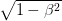 . The LTT effects, on the other hand, are first order in speed. The first order effects have been studied in the last fifty years in terms of the appearance of a relativistically moving extended body [7-15]. It has also been suggested that the relativistic Doppler effect can be considered the geometric mean [16] of more basic calculations. The current belief is that the first order effects are an optical illusion to be taken out of our perception of reality. Once these effects are taken out or ‘deconvolved’ from the observations, the ‘real’ space and time are assumed to obey SRT. Note that this assumption is impossible to verify because the deconvolution is an ill-posed problem – there are multiple solutions to the absolute reality that all result in the same perceptual picture. Not all the solutions obey SRT.
. The LTT effects, on the other hand, are first order in speed. The first order effects have been studied in the last fifty years in terms of the appearance of a relativistically moving extended body [7-15]. It has also been suggested that the relativistic Doppler effect can be considered the geometric mean [16] of more basic calculations. The current belief is that the first order effects are an optical illusion to be taken out of our perception of reality. Once these effects are taken out or ‘deconvolved’ from the observations, the ‘real’ space and time are assumed to obey SRT. Note that this assumption is impossible to verify because the deconvolution is an ill-posed problem – there are multiple solutions to the absolute reality that all result in the same perceptual picture. Not all the solutions obey SRT.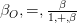 (1)
(1)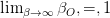 (2)
(2)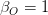 . In other words, no object can appear to travel faster than the speed of light, entirely consistent with SRT.
. In other words, no object can appear to travel faster than the speed of light, entirely consistent with SRT.
 to
to 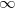 . This mapping is most obvious in its consequences. For instance, it takes an infinite amount of energy to accelerate an object to an apparent speed
. This mapping is most obvious in its consequences. For instance, it takes an infinite amount of energy to accelerate an object to an apparent speed 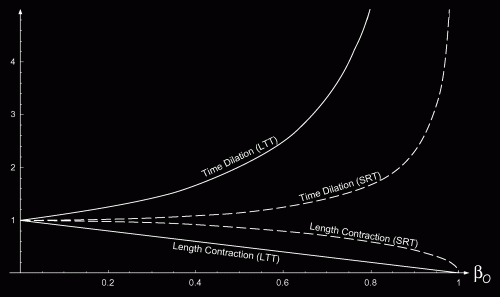
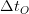 is related to the real time interval
is related to the real time interval 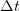 as:
as: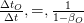 (3)
(3)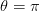 ). This observed time dilation is plotted in Fig. 1, where it is compared to the time dilation predicted in SR. Note that the time dilation due to LTT has a bigger magnitude than the one predicted in SR. However, the variation is similar, with both time dilations tending to
). This observed time dilation is plotted in Fig. 1, where it is compared to the time dilation predicted in SR. Note that the time dilation due to LTT has a bigger magnitude than the one predicted in SR. However, the variation is similar, with both time dilations tending to 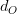 as:
as: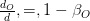 (4)
(4)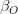 . This equation also is plotted in Fig. 1. Note again that the LTT effects are stronger than the ones predicted in SRT.
. This equation also is plotted in Fig. 1. Note again that the LTT effects are stronger than the ones predicted in SRT.

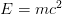 .) It says something seemingly straightforward — you can measure two complimentary properties of a system only to a certain precision. For instance, if you try to figure out where an electron is (measure its position, that is) more and more precisely, its speed becomes progressively more uncertain (or, the momentum measurement becomes imprecise).
.) It says something seemingly straightforward — you can measure two complimentary properties of a system only to a certain precision. For instance, if you try to figure out where an electron is (measure its position, that is) more and more precisely, its speed becomes progressively more uncertain (or, the momentum measurement becomes imprecise).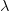 to observe the particle. The precision in the position we can hope to achieve is of the order of
to observe the particle. The precision in the position we can hope to achieve is of the order of 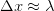 . In quantum mechanics, the momentum of each photon in the light beam is inversely proportional to the wavelength. At least one photon is reflected by the particle so that we can see it. So, by the classical conservation law, the momentum of the particle has to change by at least
. In quantum mechanics, the momentum of each photon in the light beam is inversely proportional to the wavelength. At least one photon is reflected by the particle so that we can see it. So, by the classical conservation law, the momentum of the particle has to change by at least 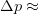 constant
constant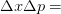 constant.
constant.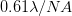 , where
, where 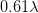 . Each photon in the light beam has a momentum
. Each photon in the light beam has a momentum 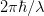 , which is the uncertainty in the particle momentum. So we get
, which is the uncertainty in the particle momentum. So we get 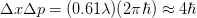 , approximately an order of magnitude bigger than the quantum mechanical limit. Through more rigorous statistical arguments, related to the spatial resolution and the expected momentum transferred, it may possible to derive the Heisenberg uncertainty principle through this line of reasoning.
, approximately an order of magnitude bigger than the quantum mechanical limit. Through more rigorous statistical arguments, related to the spatial resolution and the expected momentum transferred, it may possible to derive the Heisenberg uncertainty principle through this line of reasoning.