| The following sections (and figures) have been abridged out of this post. The full version of the article is available as a PDF file. () |
3 LTT Effects for Approaching Objects
3.1 Asymmetric Effects
3.2 Time Contraction and Length Expansion
3.3 Higher-Order Perceptual Effects
4. Explanations Based on LTT Effects
4.1 Twins Paradox
4.2 Superluminality and Causality
4.3 Superluminal Motion
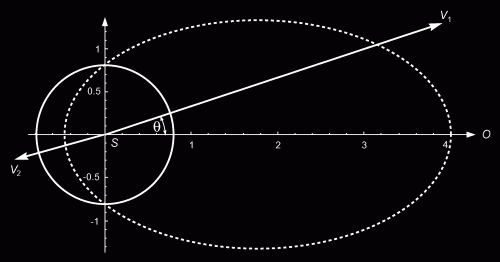 |
| Figure 2. Illustration of the traditional explanation for the observed superluminal motion. An object expanding at a speed ratio = 0.8, starting from a single point S. The solid circle represents the boundary one second later. The observer is far away on the right hand side, O (at infinite distance). The dashed ellipse is the apparent boundary of the object, as seen by the observer. |
4.4 Symmetric Radio Sources
 |
| Figure 3. The radio jet and lobes in the hyperluminous radio galaxy Cygnus A. The hotspots in the two lobes, the core region and the jets are clearly visible. (Reproduced from an image courtesy of NRAO/AUI.) |
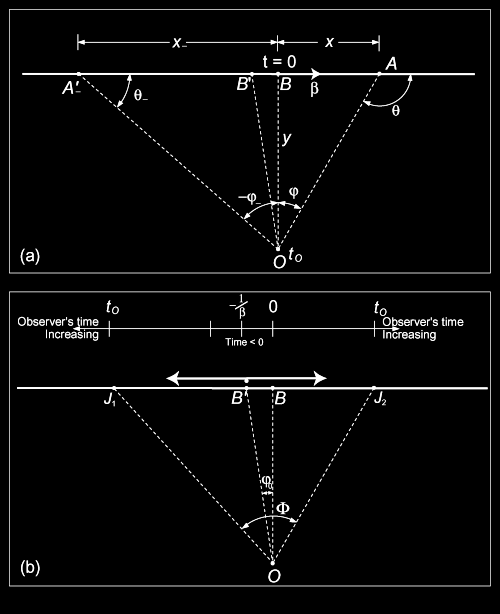 |
Figure 4. The top panel (a) shows an object flying along 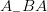 at a constant superluminal speed. The observer is at at a constant superluminal speed. The observer is at  . The object crosses . The object crosses 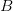 (the point of closest approach to (the point of closest approach to 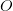 ) at time ) at time 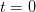 . The bottom panel (b) shows how the object is perceived by the observer at . The bottom panel (b) shows how the object is perceived by the observer at 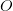 . It first appears at . It first appears at 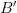 , then splits into two. The two apparent objects seem to go away from each other (along , then splits into two. The two apparent objects seem to go away from each other (along 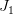 and and 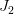 ) as shown. ) as shown. |
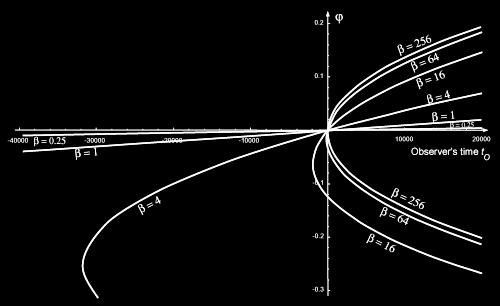 |
Figure 5. The apparent angular positions of an object traveling at different speeds at a distance 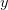 of one million light years from us. The angular positions ( of one million light years from us. The angular positions (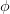 in radians) are plotted against the observer’s time in radians) are plotted against the observer’s time 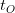 in years. in years. |
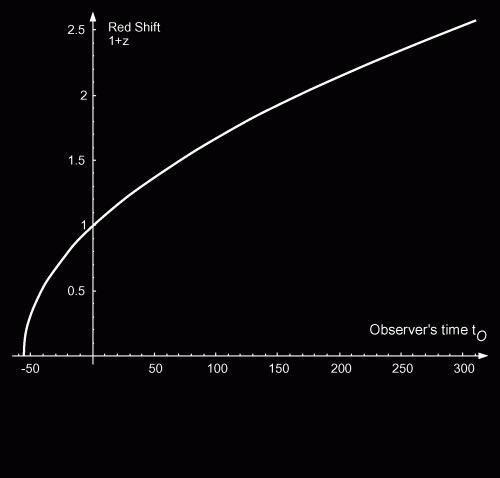 |
Figure 6. Time evolution of the redshift from a superluminal object. It shows the redshifts expected from an object moving at 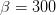 at a distance of ten million light years from us. The X axis is the observer’s time in years. (Since the X axis scales with time, it is also the redshift from an object at 116 light days –ten million light seconds–with the X axis representing at a distance of ten million light years from us. The X axis is the observer’s time in years. (Since the X axis scales with time, it is also the redshift from an object at 116 light days –ten million light seconds–with the X axis representing 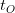 in seconds.) in seconds.) |
