Philosophy, Physics, Science

Interpretation of Special Relativity

The safer, easier way to pay online.
"Particles and Interactions" is available as a beautifully designed printable eBook compatible with mobile devices. Get it now for $5.49 for immediate download!

When we looked at Quantum Mechanics, we talked about its various interpretations. The reason we have such interpretations, I said, is that QM deals with a reality that we have no access to, through our sensory and perceptual apparatuses. On the other hand, Special Relativity is about macro objects in motion, and we have no problem imagining such things. So why would we need to have an interpretation? The answer is a subtle one.

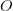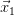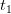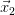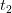What do we mean when we say we observe an object in motion? Let’s say we are at a position, say, O. The object is at position \vec{x}_1 at time t_1, and at \vec{x}_2 at t_2. Although most people may not notice it, in the last sentence, I already embedded an unreasonable number of assumptions about space and time, which will become clear very soon.
Here are three possible views we could have when we make a statement about its speed.

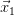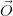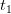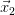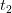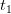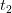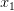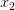  1. We could say that when the object is at \vec{x}_1, it emits a ray of light, which reaches us at \vec{O} at time t_1. Similarly for \vec{x}_2 and t_2. Note that we are defining t_1 and t_2 (and assuming what x_1 and x_2 mean) with this statement. Then the velocity of the object becomes 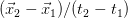(\vec{x}_2 - \vec{x}_1)/(t_2 - t_1). We will call it the perceived velocity. It is how the object appears to move, from our perspective.
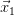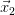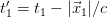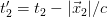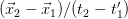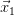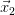  2. Another thing we could say is this: Since we know that light takes a certain amount of time to reach us from \vec{x}_1 and \vec{x}_2, the real time for the object is and . And then the real velocity would be . Let’s call this quantity its absolute velocity, or its velocity in the absolute reality. Note that we are again assuming what \vec{x}_1 and \vec{x}_2 mean, but handling the time at the object a bit better.
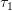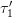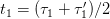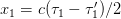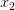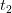  3. A third way of looking at it is this: Let’s say we send out a pulse of light to the object at time \tau_1. It gets reflected back to us at our time . So, at time , the object is at a distance . If the object is going directly away from us (this is important), we can define another distance x_2 at t_2 in exactly the same way. Then its speed would be (x_2 - x1_)/(t_2 - t_1).

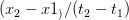Special Relativity takes the third view (or something very close to it). Based on this view, SR defines a coordinate transformation between two frames of reference. But having done that, it insists that the transformation is real, and not a perceptual effect. And, this is the subtle point, we still have to do computations of the kind described in the view number 2 above in order to understand motion. Since this post is meant for a non-technical crowd, I won’t belabor the point, but how it pans out mathematically is quite interesting.

Here is a real lecture on the co-ordinate transformation part of SR by Prof Susskind of Stanford. Although it looks formal and rigorous, it does have the same subtle issues. If you watch the derivation of the transformation from 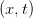(x, t) to 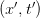carefully, from around the timestamp 47:05 in the video, you will see that he makes the statement 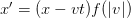and 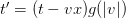. This statement is true only on the 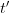axis and 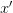axis (or when 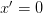and 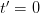) respectively, which he explicitly states, but then he silently goes on to assume it is true for all 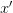and 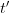. In other words, what is written is the same as 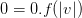0 = 0 . f(|v|) and 0 = 0 . g(|v|). 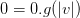It does not follow that 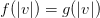f(|v|) = g(|v|). So the coordinate transformation is derived with insufficient mathematical or physical reasoning.

In the original paper, Einstein sweeps this difficulty under the rug by saying that it follows from the obvious isotropy we ascribe to space, despite the fact that space is not isotropic in SR coordinate transformation; it contracts only in the direction of motion. This is why I added the caveat that the third view of speed and motion applies only when the object is flying away from the observer — it is speed, a scalar, not velocity, the vector. I believe there is another way of deriving a different set of transformation rules without using a non-existent isotropy argument.

My belief is that one has to decouple the constancy of the speed of light (and the resultant covariant transformation of space-time as required by Maxwell’s equations) from the perceptual effects of light travel time. Such an approach would be equivalent to developing a framework based on second one of the views of speed and motion listed above. I did this in my book and my published papers. In fact, I went one step further, and investigated the nature of space, and what we mean by it — space is a cognitive model created in our brain and mind to represent the electrical signals generated by light falling on our retinas. Let me quote Einstein again.


Developing a new framework, however, is tantamount to redefining the whole of modern physics based on a different theory of relativity. It is a tall order.

Comments