In this section, we will try to look at the historical origin of Quantum Mechanics, which is usually presented succinctly using scary looking mathematical formulas. The role of mathematics in physics, as Richard Feynman explains (in his lectures on QED given in Auckland, New Zealand in 1979, available on YouTube, but as poor quality recordings) is purely utilitarian.
Suppose you give, say $10 to your son to buy a few things. When you get the change back, you want to make sure that the shop clerk didn’t cheat him. So you add up the prices, and calculate the balance. It may take you a minute or two to do it if you are away from your calculator or smart phone. What you have done, using primary school arithmetic, is the equivalent of taking 10,000 pennies, counting the pennies used for each item and removing them, and then counting what is left. You don’t do all the penny counting because you know a better and more elegant way of doing it. Similarly, physicists use mathematics to keep tab of various numbers and quantities. According to Feynman, however, what is much more important than the formulas is to understand what it is that they are keeping track of and why; and not so much how.
With Feynman’s insight in mind, let’s take a look at the physics of small things. By 1900, there were indications why classical physics was incomplete. Here are three things that classical physics couldn’t handle at all.
Blackbody Radiation
A blackbody is an opaque, non-reflective object that absorbs all the light (all electromagnetic radiation, rather) that falls on it. It reemits radiation based on its temperature. At room temperature, the emission is in the infrared region, and the object emits little any visible light – hence blackbody.
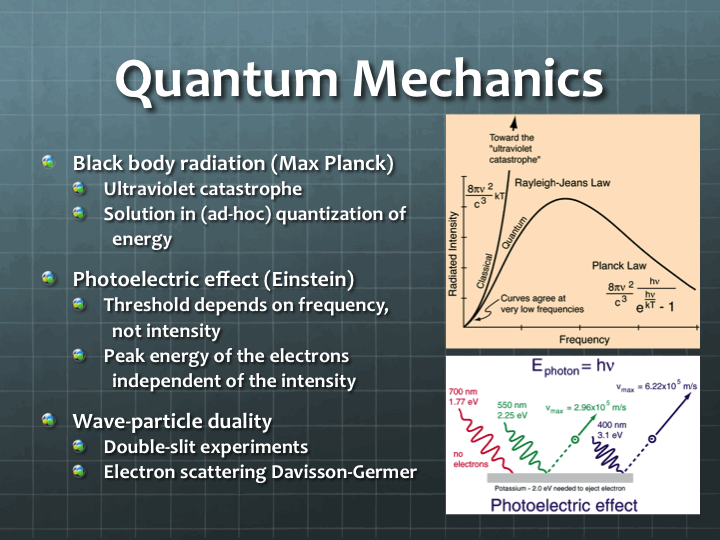
It looked as though classical physics had all the tools necessary to calculate the emission spectrum (how much energy is emitted at each frequency). Here is the gist of the calculation. A blackbody can be thought of as a chamber, like a tiny hollow cube with a hole in it. The inside walls of the cube are painted black. The frequencies of the emitted radiation then correspond to the standing waves you can create in the chamber, a bit like the notes you can create on a guitar string. You have the fundamental frequency of the chamber, and then the higher harmonics. As you can see, there are an infinite number of higher harmonics that can create as standing waves in the cavity. The trouble in the classical picture was that each of these standing waves corresponded to a mode of emission. And you had the so-called equipartition theorem that said all modes should have the same energy depending on the temperature. In other words, you would get an infinite amount of energy at the higher end of the frequency spectrum. The higher end corresponds to light in the ultraviolet region and beyond, and hence this quandary was called the ultraviolet catastrophe.
Of course, no body – however black – emits an infinity of anything. So this description and, by extension, classical physics had to be wrong. The resolution to this catastrophe came when Max Planck postulated (without much scientific justification) that the energy of each radiation come in discrete packets depending on the frequency – the higher the frequency, the larger the size of this energy quantum. This meant that it would take more energy to generate a higher mode, and therefore it is less likely. Using this assumption, Planck was able to derive the shape of the emission spectrum that matched the observation very well. In other words, the quantization of energy got rid of the catastrophe, albeit with little physical justification.
Photoelectric Effect
The justification came in the form a Nobel willing paper by Einstein in 1905. He took the idea of energy of light (or electromagnetic radiation, in general) coming in discrete packets (or being quantized, to use the proper term) and described how photoelectric effect worked.
Photoelectric effect is the generation of electricity when light falls on some metals. You use this effect every time you use a remote control – the infrared light from your remote hits the sensor in your TV (which is a photoelectric material) and generates a signal. Digital cameras and solar cells also work using the same underlying principle.
Classical physics had a hard time describing the photoelectric effect. In the classical picture, light is made up of waves. So light hitting the electrons in a metal is similar to a wave hitting the pebbles on a beach. An intense wave, say a Tsunami, hitting the beach should make the pebbles go gangbusters and create a huge amount of electricity. In experiments, the intensity of the radiation had no bearing on the onset of photoelectric effect. But its frequency did, which makes perfect sense if you assume, as Planck did for the blackbody explanation, that the energy of the radiation is proportional to its frequency. Einstein was able to calculate the details of the effect using this assumption, and went on to call these quanta of energy photons. Thus, light is made up of particles (photons) whose energy depends on the frequency.
Einstein’s explanation, and the acceptance of energy quantization as a real and physical, paved the way to the development of Quantum Mechanics. So, it is strange that he could not come to terms with it in his later years.
Wave-Particle Duality
The moment you start thinking of light as particles, however, you run into other problems. Light has properties that are perfectly wavelike – like interference, reflection, diffraction etc. As though that wasn’t bad enough, soon electrons, bona fide particles that they are, were shown to behave like waves.
In x-ray crystallography, the atomic arrangements of a crystal are deduced from the pattern of light bouncing off of it. This can work only if the entity hitting the crystal has clear wave-like properties. In scattering experiments where electrons were bombarded against a nickel crystal (Davisson-Germer experiment), clear wavelike patterns were created, proving electrons were waves too. There were interference (double-slit) experiments (probably thought experiments) with electrons, as described in Feynman’s lectures, which also prove the wave nature of particles.
So it turned out that particles and waves are somehow mixed. They were both at the same time. Rather, the wave nature and particle nature of they underlying entity comes through under the right circumstances. At a very small scale, matter is neither particle nor waves, but something that can manifest itself as either.
Since this post has grown bigger than I expected, I will have one more post on Quantum Mechanics, where I describe how it is used in physics, as well as my own take on how it should be viewed.


