When we hear about Einstein and the special relativity (or the special theory of relativity, to use the real name), we think of the famous 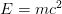 equation, and weird things like the twin paradox. While those things are all true and important, the problem SR tries to solve is a completely different one. It is an attempt to defend a basic principle in physics.
equation, and weird things like the twin paradox. While those things are all true and important, the problem SR tries to solve is a completely different one. It is an attempt to defend a basic principle in physics.
The basic principle of relativity is that the laws of physics do not change when you move without acceleration. In other words, motion at a constant velocity is indistinguishable from being stationary, which is why you may have had this illusion while in a stationary train on a platform that you are moving, when the train next to you starts moving. Whatever experiments you can do will not tell you whether you are standing still or moving.
If you think about it, it has to be this way. If there were only two objects in the universe, it wouldn’t make any sense to say which one is moving. Only relative motion has physical significance. Associated with each moving object is a coordinate system, or a frame of reference, called an inertial frame. All inertial frames are equivalent, which is considered a symmetry in physics and is called the principle of relativity.
Symmetries and Conservation Laws
Now, let’s take a short timeout to talk about symmetries in physics. When you hear the word symmetry, you think of objects that look the same when you rotate them or flip them. In physics, this idea is taken a bit further. The fact that the laws of physics do not change when you try them at a different place is also a symmetry of nature, called translational symmetry.
There is a mathematical principle called Noether’s theorem, which states that whenever you have a symmetry, you will find a corresponding conserved quantity. Translational symmetry and the conservation of momentum are related through this theorem. Another symmetry is that the laws of physics are invariant over time (which is a good thing, otherwise we don’t have any business calling them “laws”). This symmetry has a corresponding conserved quantity, which is energy. This mathematical fact is the reason why you cannot patent a perpetual motion machine. It violates the conservation of energy. If it actually did work, it would mean that the laws governing it would not be time invariant. In other words, it might not work tomorrow.
The symmetry of indistinguishability of inertial frames (the principle of relativity) in motion is true of electricity and magnetism as well. By the way, I don’t know what the corresponding conserved quantity is, but I suspect it is the length of space or space-time vectors, depending on whether you use pre-Einstein (Galilean) or post-Einstein (Lorentz) relativity. A coil moving next to magnet generates electricity. The amount of electricity generated depends only on the relative velocity, doesn’t matter whether you move the coil or the magnet. So the principle of equivalence of inertial frames holds for electricity and magnetism as well. Electromagnetism is described in Maxwell’s equations (relating space and time variations in electric and magnetic fields to currents and charges) should be “covariant” – meaning, it should change in the same was as the coordinates transform. Otherwise, microwave ovens would work differently on an airplane.
One solution to Maxwell’s equations is EM waves (light) moving at its speed. The covariance of these equations means that the speed of light has to be the same constant when measured in any inertial frame. Based on this observation, Einstein postulated that the constancy of the speed of light is a basic law of nature. Once you accept this postulate, we have to accept that it does not change when measured in different inertial frames. In order for this speed to be a constant, space and time will have to change instead. We will delve into this constancy, both in terms of physics and philosophy, in the next section.