In this post on Quantum Mechanics (QM), we will go a bit beyond it and touch upon Quantum Field Theory – the way it is used in particle physics. In the last couple of posts, I outlined a philosophical introduction to QM, as well as its historical origin – how it came about as an ad-hoc explanation of the blackbody radiation, and a brilliant description of the photoelectric effect.
The main takeaways from those two posts are:
- Don’t get too caught up on what it is that QM is describing because it doesn’t correspond to a reality that we can perceive or imagine.
- Accept the fact that subatomic particles are not at all like little balls of matter. I want to harp on this point for one last time. In biology, when you break up a live cell, what you get are dead chemicals. In chemistry, when you break up a compound molecule, you get elemental atoms with vastly different properties. Similarly, when it comes to particles physics, the particles that make up atoms are nothing like atoms or matter. They obey Quantum Mechanics though.
- Think of Quantum Mechanics as a mathematical framework mapping the features of an unknown reality (the world of particles) to macro effects that you can measure or make use of in the real world.
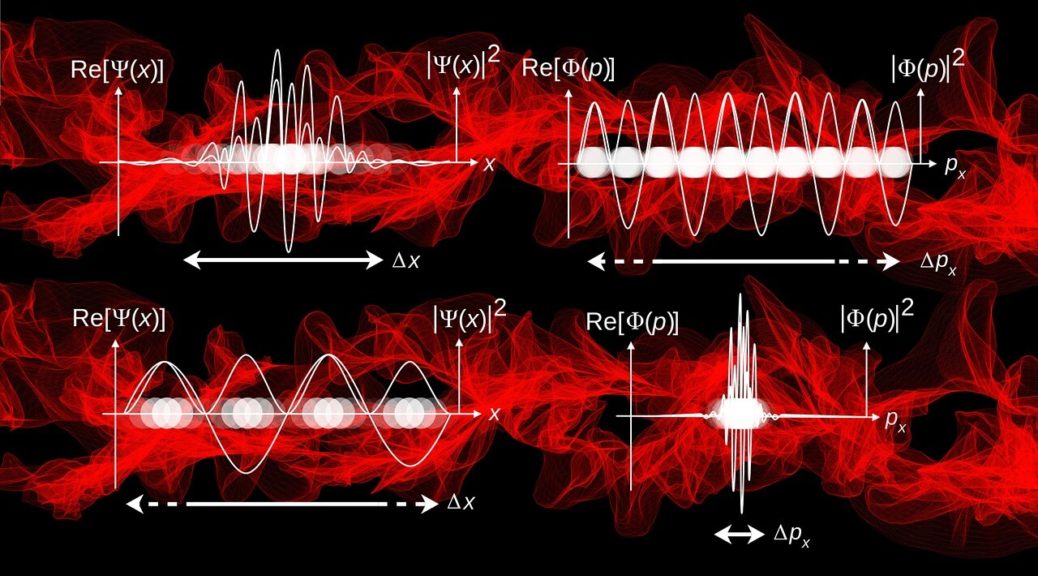
Because Quantum Mechanics is a mathematical framework, and I am going to describe it in words, the rest of the post is going to be a bit vague. In the QM picture, you cannot think of particles as point-like, or even matter-like. Particles obey, or are spread out, like a wave. Now, when you think of a wave, you imagine ripples in a pond. So for particles, you might ask, what is it that is waving? Is it the probability of finding them in space? Or is it their mass itself? Don’t ask such questions.
What is waving is a mathematical entity called probability amplitude, from which probabilities can be computed. Probabilities of what? Of any macro level properties that you are looking for, like position, momentum, energy etc. What you have is the so-called wave function, which fully describes the particle and the system under investigation. This wave function is the solution of some particular physical conditions – stating something like systems with high energies tend to evolve fast.
Now, resist the temptation to think of it as if the particle has an associated wave function, or it obeys one. Rather, think of the wave function as a complete description of the particle under that condition. It is as complete as it is going to get. Once you have the wave function of one physical property (say the location of the particle), if you want to know another property (say its momentum), you apply an operator to transform the wave function.
While a single particle is an interesting theoretical problem to study, an interaction requires at least two particles. So, when I said particle physics required an understanding of Quantum Mechanics, I wasn’t being totally honest. It requires a bit more than that. What happens when you have multiple particles? In classical physics, such situations are modeled by fields, which can handle action at a distance.
If you have two positive charges, for instance, we think of them having an electric field which exerts forces on them causing them the repel each other. In the QM picture, fields also become operators acting on combined wave functions, and this extension is called Quantum Field Theory. It is horribly complicated mathematically, but doable using Feynman diagrams and formulation.