[This post is my translation of an excellent short story by one of the most gifted storytellers of our time, O.V.Vijayan. The translation from Malayalam is a feeble effort, because such distant translations are not merely between languages, but cultures. The untranslatable expressions are marked with asterisks. Enjoy!]
Reached Kanjikad from Palghat by Coimbatore street. From there on, it was unpaved dirt road to the mountains. Even the rough taxi Jeep found that hard to take. This was Theyunni’s second trip here in the last ten years and he had no complaints about the roughness now.
“Ditch ahead”, Driver said, glancing at the dirt road in front.
“If you want to stop here, it’s okay”, Theyunni offered, “I can walk.”
It’s about two miles from here. Accustomed as he was to the comfort of limousine rides between airports and star hotels, the prospect of the hard hike did not discourage Theyunni.
“Nah. We’ll go slow, sit tight.”
“Okay.”
The Jeep carefully negotiated the winding mountain road. Theyunni glanced at the wild valley as if for the first time. The sunshine cooled by the hillside, the east winds tunnelled through the mountain passes and roaring towards Palghat…
“The trees are all gone, aren’t they, Driver?”, Theyunni observed.
“All downed. Was forests here till about five years ago. Elephants used to come down.”
Yes, last time when he was here, there were huge trees on either side. Trees he didn’t know the names of. There were crickets all around carrying on with their shrill orchestra. Theyunni recalled that journey. He was coming back to Bombay after a European trip and his wife was at the airport. She said, “There is a letter from home, looks like *Brother’s handwriting.”
“Wonder what is happening. Didn’t you open it, Phoebe?”
“You know I don’t open your letters.”
When the car was moving towards Juhu, Theyunni stole a glance at Phoebe’s face behind the wheel. Like a flawless marble sculpture with golden hair dancing in the wind. It was against her culture to open her husband’s letters. There were many things in her culture that attracted him — her confident courage in kissing him in that garden few years ago, proclaiming, “I love you”. If the relationship were to turn sour in the years to come, the honesty and integrity that would make her say, “I do not love you any more, we have to get divorced”. These were the challenges that inspired him. He remembered the journey home to tell *Father that he was in love with Phoebe, his fellow-student at Stanford. Father did not say anything against it, just smiled his sweet, thoughtful smile. It was *Mother — “We had Devaki’s horoscope looked at…”
Devaki was a distant relative. The daughter of some in-land farmer. Hiding his contempt for horoscopes, Theyunni comforted Mother, “That is not much, Mother. We didn’t give our word.”
Nobody said anything for a while. Then Mother said, “Isn’t understanding as big as word? It’s like Devaki has married you in her heart.”
“It’s the boy’s decision, Madhavi,” Father said, “Why do you want to say this and that?”
Mother withdrew herself, “I didn’t say anything…”
“Don’t worry about Mother’s complaints, Kutta. So, do you like this Phoebe?”
Theyunni was a little embarrassed, “Yes.”
“Will an American girl like to live in this old family house of ours, Kutta?”, Mother inquired.
“Why wouldn’t she?”
Father said, “It’s not as though they are going to come live here, is it?”
“So Father and Son have decided that as well,” Mother said, “that they don’t want to live here?”
“Wherever we live, we’ll come here first, Mother.”
Theyunni saw Mother’s eyes well up. After blessing Phoebe and wishing Devaki well in her life, Mother said, “I won’t ask you to change your mind. But, will you look after Father, Kutta?”
“Of course.”
“You remember how he used to be? His body is getting old…”
Father intervened again with his smile, “Madhavi, why do you say such things and make him unhappy? Don’t pay any attention to her, Kutta.”
Even during the novelty of his love, Theyunni could feel *Devaki’s true meaning in his *rustic heart — the farmer bride who would sweep the floor and light the evening lamp. Mother said, “There was only one thing on my mind — your sister-in-law is not able-bodied. If it had been Devaki, there was a hope that she would look after your father in his old age…”
Theyunni didn’t say anything then. Even in the later years, he couldn’t say anything about that. Phoebe, who never opened her husband’s letters, drove skillfully through the streets of Juhu. When Father fell sick years after the marriage, Phoebe advised, “Your little town is actually a village. Why don’t we take him to a good hospital in a city? We can easily afford that.”
What Father needed was nearness and touch to die peacefully. Theyunni came home alone with those and saw him off. Mother also died in the old family house. Phoebe was back at Stanford then. She sent a formal condolence telegram. *Devaki‘s meaning again filled his mind.
In Juhu, Theyunni read Brother’s letter. “I’m not doing too well, Kutta. Just to let you know. I won’t ask you to take time off your busy schedule and come by these forests. Just think of me, same effect as seeing. Didn’t even let Sreekumar know. I was worried that he might get anxious and take a trip — not easy to come here from Cambridge, is it? If only your sister-in-law had been alive… Weaknesses of an old heart…”
The Jeep continued it’s laborious journey negotiating an occasional ditch and gutter.
“Sorry about the trouble, Driver,” Theyunni tried to comfort the driver.
“Nah, just doing my job.”
Must be another mile from here. It was after his wife’s death that Brother decided to resign from service and move to the high lands. Theyunni vehemently opposed that decision. “Why are you moving to this god-forsaken land in Palghat among leopards and wild boars? Moreover, you could be in service for another 10 years. Even after retiring, you know that a nuclear physicist can do so many things…”
Brother’s reply came, “There are debts that one owes — to one’s country, one’s community, one’s family. I feel that I have repaid my dues to the best of my ability. There are some other obligations that I have to take care of. That’s is why I’m seeking refuge in these valleys.”
Brother never mentioned what those obligations were. Theyunni didn’t inquire either.
The soft-spoken Brother took a decision only after much reasoning; it was not easy to make him go back on them. Later, Brother wrote about his camp-site: about four miles off the road, there were fertile lands lying just outside the woods. Brother built a house there, among coconut palms, vegetables, mango trees… Dirt walls, wooden ceiling and roofs of clay tiles. It was at some distance from anywhere. However, there was a farmer, Ponnuswami, living in a hut nearby. Brother could ask Ponnuswami for help if needed. Apart from that, he was quite alone in that valley. Theyunni could not figure out the meaning of that penance and forgot about it. Years went by. But when Phoebe handed over that unopened letter, he suddenly felt that he should go there in a hurry.
“Well, Phoebe, I’ll go and see what’s going on.”
“What is the name of that place? Kanjikad, isn’t it?”
“Yes.”
“Brother had invited me to go and see the mountains.”
“Yes, I remember.”
“Must be a perfect place for get-away vacation. But it’s dangerous to get sick there. Why don’t you bring him here? We could have him treated at Jeslock or something.”
Phoebe was repeating her suggestion on treatments. Theyunni remembered the last time the suggestion was offered and it made him uneasy.
“We can’t get inside his mind, Phoebe. I’ll go there and see.”
That was how Theyunni came here for the first time, ten years ago. Not only was he anxious about Brother’s health and solitary life, he also wanted to give Brother a piece of his mind about the untimely penance. When he took a taxi from Coimbatore airport to go to Kanjikad, his mind was filled with impatience and hard feelings towards Brother. The driver got discouraged by the sight of ditches and gutters in the dirt road. It didn’t take too much to provoke Theyunni.
“I could break the axile if I drove up this way,” complained the driver who was Tamil.
“How much does this stupid car of yours cost?”
“Sorry Sir, didn’t mean to…”
“If your car breaks, let it break. I’ll give you what it costs. Drive.”
When he got off the car, Theyunni saw Brother taking a walk in the field — looking bright and healthy.
“Why did you come all this way, Kutta?”, Brother commented on the advisability of the trip.
“You can say that. Living in the forests, writing letters about getting sick, how could I ignore it?”
“Come in.” Brother took him inside the house.
Theyunni looked around and found everything unsatisfactory. “Why do you punish yourself like this?”
“Do I look as though this is punishment?”
Nobody said anything for a while. Then Theyunni inquired, “Who treated you while you were ill?”
“Teat?! Nobody!”
“What am I supposed to say about that?”
Brother smiled, “You don’t get it, do you, Kutta?”
“What do you do for food?”
“I have asked Ponnuswami’s wife to show up. To cook something for you. Me, this is all I eat.”
He pointed to the husks of two young coconuts in the basket. “That was breakfast. Two more for dinner.”
“That is you diet?!”
“Not just diet, medicine as well!”
When it got dark, Theyunni wanted to know, “Brother, what if some thieves show up?”
Brother laughed heartily, “Four white *mundu, four cotton shawls, two towels and some clay pots. That’s all this house holds. The thief is quite peaceful by nature, it’s our avarice that makes him do this and that!”
After dinner, they laid down to sleep — on the floor, on sleeping mats. For Theyunni, it was the first time in a long while without the air conditioner. The winds roared outside the house. Through the mountain passes, like the loud waves in an uptide.
“Kutta”
“Yes, Brother?”
“You hear that?”
“The winds, right?”
“Yes, but to you hear them?”
“Yes, I do. Why do you ask?”
Brother was silent for a while in the darkness. Then he said, “No, you don’t hear them.”
It was with the same dissatisfaction at Brother’s life in the wilderness that Theyunni went back to Bombay. Brother said, seeing him off, “It was a mistake, Kutta. A weakness. Felt like writing to you when I was ill; I won’t bother you like this again. There aren’t any illnesses that these valleys can’t cure. And if there are, do humans have medicines for them?”
Now, it was ten years after those words that Theyunni was coming back. Phoebe was not with him any more. She showed her natural honesty and told him that the love between them had dried out. Theyunni did not fly from Bombay. He took the train to Palghat along with numerous other people. Like in his childhood, in second class. Two day journey. Hills and woods and rivers and villages slowly went by in the window as the train ambled towards Palghat. The old family house was no longer there. So he rested in a hotel and set out for Kanjikad the next morning. His gruffiness during the last journey ten years ago had disappeared now. Theyunni felt that his peacefulness was spreading to the fellow passengers and even the landscapes.
The Jeep driver also was friendliness personified.
“Hard trip, isn’t it, Driver?”
“Nah, we are quite used to these. A little worried about your trouble, that is all.”
Brother’s fences and steps appeared at a distance.
“Over there, Driver.”
“Isolated house, isn’t it, Sir?”
“Yes.”
Ponnuswami was waiting by the house. He stepped down to welcome Theyunni. They looked at each other; Ponnuswami wiped his tears.
“He had asked me not to telegram, that is why I wrote a letter instead.” Ponnuswami said, “I am sorry.”
“Not at all, you were respecting Brother’s wishes. I understand.”
Ponnuswami walked over to the backyard. There was a small plot where a Thulasi plant was beginning to take root. Ash remnants of the pyre around it.
“This is it,” Ponnuswami said. “The bones were dropped in the Peroor river. If there are some other rituals you want to do… But,…”
“Yes, Ponnuswami?”
“He said that no rituals were necessary. That he had uprooted the rituals. I am not educated, just thought that he was talking about some sacred state.”
“That must be what he meant.”
“Is Sreekumar coming up?”
“I had telephoned him from Bombay. He is not coming. He had told me one thing — that this land and house are for you.”
Ponnuswami had gone beyond such earthly things. “He also had told me the same thing; I didn’t want to tell you. But, I don’t need any of this. You or Sreekumar could sell these…”
“Brother’s wishes, Ponnuswami. We must respect them.”
“Well, if you insist.”
“How many children do you have?”
“Four.”
“Well, this will be a good place for them to grow up in.”
Ponnuswami bowed once again, “If you ever want to come back and live here, my family and I will get out of here for you.”
“That won’t be necessary, Ponnuswami.”
I don’t deserve to live here, Theyunni said to himself. They got back into the house.
“You take rest. I will get you a young coconut from the fields.”
“The driver is waiting in the Jeep outside. Ask him to come inside and have something to drink.”
When Ponnuswami brought the young coconuts, Theyunni said, “You can go home now, if you like. I’m fine.”
Ponnuswami left. Theyunni said to the driver. “Do you think you can stay here overnight?”
The driver expressed his disagreement through silence.
“Didn’t plan that way when we set out,” Theyunni said. “This is Brother’s house. I came here because he died, couldn’t get here before.”
The driver turned attentive. Theyunni continued, “Feel like sleeping here for a night.”
The driver’s disagreement melted away silently. “I can stay.”
“I can pay you whatever you want for staying.”
“That won’t be necessary.”
Time turned red and went down on the hilltops. Theyunni went inside and went through Brother’s wooden box. Three white mundu’s, laundered, three cotton shawls and two towels. Theyunni’s sadness dripped into them. When he went to bed, he was not sad any more, a kind of gratified grief. A fulfillment of love and traditions. He slept with the childhood dreams of fairy tales. Late in the night, he woke up. He listened to the music of the winds. After this night, it would be the trip back to the city. Theyunni could feel Brother’s kindness in the winds. The winds muttered the unknown *Manthras that marked the end of that kindness and life, some *distant baby voices… A night full of sacred whispers, this was the *justification of lifetime.
Theyunni listened to the whispers and slept, awaiting the morning.




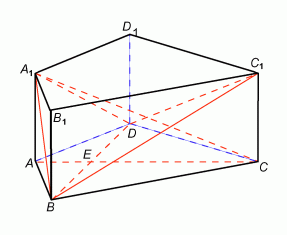
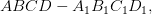
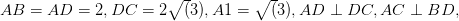 and foot of perpendicular is
and foot of perpendicular is 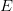 ,
,
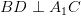
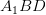 and
and 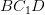
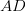 and
and 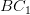 which are in different planes.
which are in different planes.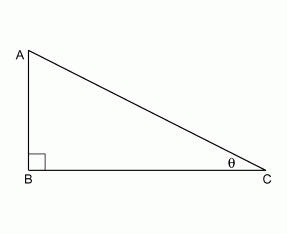
 is a right angle,
is a right angle, 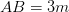
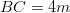
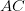 ?
?

![[casual picture]](/img/kandm1-ss.jpg) Just before 1970, they (and me, which makes it we I guess) moved to Trivandrum, the capital city of Kerala. I lived in Trivandrum till I was 17. Lots of things happened in those years, but since this post is still (and always will be) work in progress, I can’t tell you all about it now.
Just before 1970, they (and me, which makes it we I guess) moved to Trivandrum, the capital city of Kerala. I lived in Trivandrum till I was 17. Lots of things happened in those years, but since this post is still (and always will be) work in progress, I can’t tell you all about it now.![[Wedding picture]](/img/kandm2-ss.jpg)
![[Anita Smiles]](/img/anita1-s.jpg)
![[Neil Smiles more!]](/img/neil-s.jpg)
![[Dad]](/img/dad.jpg) Later on, in 2007, I moved to
Later on, in 2007, I moved to