A discussion in the Science Forums on the appearance of a laser dot on a ceiling. It is thought that if you pointed a laser dot on a ceiling and turned the laser gun fast enough, you could create superluminal laser dots. Could you, really?
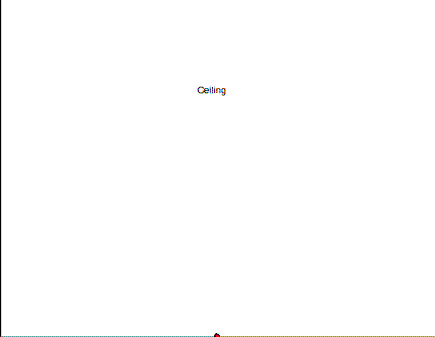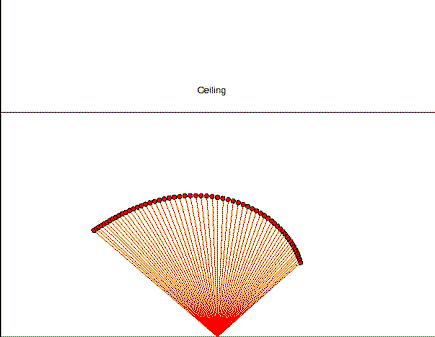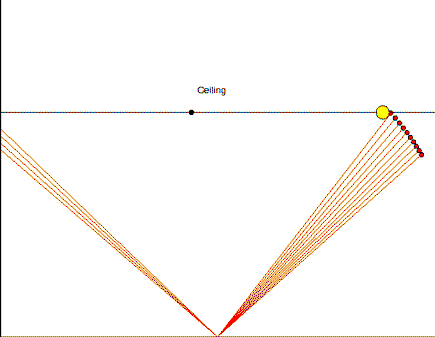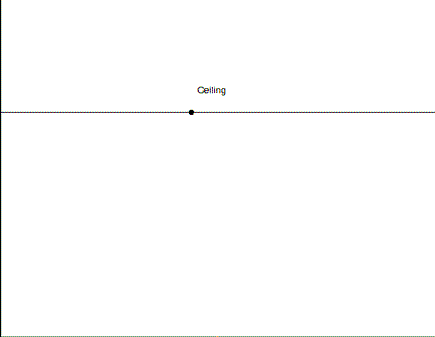
In the animation above, the laser pointer is at the bottom-center of the figure. I’m turning it so fast that the laser dot on the ceiling should travel at 10c (which is indicated by the white circle moving across the ceiling.) But it takes a while for the laser to reach the ceiling. The light is indicated by the small red dots which move towards the ceiling (10 times slower than the white circle). The dot appears when the light hits the ceiling.
As you can see, the light from the laser first hits the ceiling at a point close to the top (indicated by the black dot), and subsequently, light on either side starts hitting the ceiling, making two dots (in yellow and green). This is the how one laser pointer creates two dots appears at two places at the same time. Note how the dots slow down considerably as they move away from the center. Light travel time effects dominate at shallow angles.
But CPL.Luke is right. If the ceiling was a spherical shell and the laser was at its center, there would be only one dot moving at 10c. (At least, that’s what I get when I try to work it out.) In effect, by having a spherical ceiling, you are cutting out the shallow angles; the laser is always perpendicular to the ceiling. In this case you can treat the laser as a solid rod, but with a constant delay equal to r/c (which differentiates to zero, thus not affecting the speed of the dot).
If a superluminal object did exist, would it appear as two identical objects to us?
Okay, I will start with an animation first to make it interesting. I will post the notations and algebra in the next post.
In the figure below, we have a (purely hypothetical) superluminal object – the white circle flying across the animation at ten times the speed of light. As it flies by, it emits light. We consider the light rays (the red lines with small red circles at the end) coming towards the observer at the bottom-center of the animation. As we can see, the first ray of light that reaches the observer is emitted at a point close to the point of closest approach to the observer, indicated by a black dot that appears when the ray reaches him, say at time 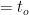 . The rays emitted before this first ray reach the observer after
. The rays emitted before this first ray reach the observer after 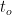 . This reversal of the order in which the rays reach the observer gives rise to the perception of two objects moving away from the black dot. (If the object doesn’t change during its flight, the two “phantom” objects are identical to each other.)
. This reversal of the order in which the rays reach the observer gives rise to the perception of two objects moving away from the black dot. (If the object doesn’t change during its flight, the two “phantom” objects are identical to each other.)

Now, my question is, if we see two objects in a symmetric formation in the night sky, can we be sure that they are really two, and not our perception of one object in motion? Of course we can if we say that nothing can really travel faster than light. Assuming hypothetically that we didn’t know about SR and its constraint on the speed, is there any way we could work out the “real” speed from our observation of the rate of angular separation? My feeling is that there are at least two configurations (one superluminal object going in one direction or two objects – superluminal or otherwise – going in opposite directions) which will result in the same observation.
Algebra behind the animation
This post gives the algebra behind the animation. First, let’s define the notations used using the following figure.
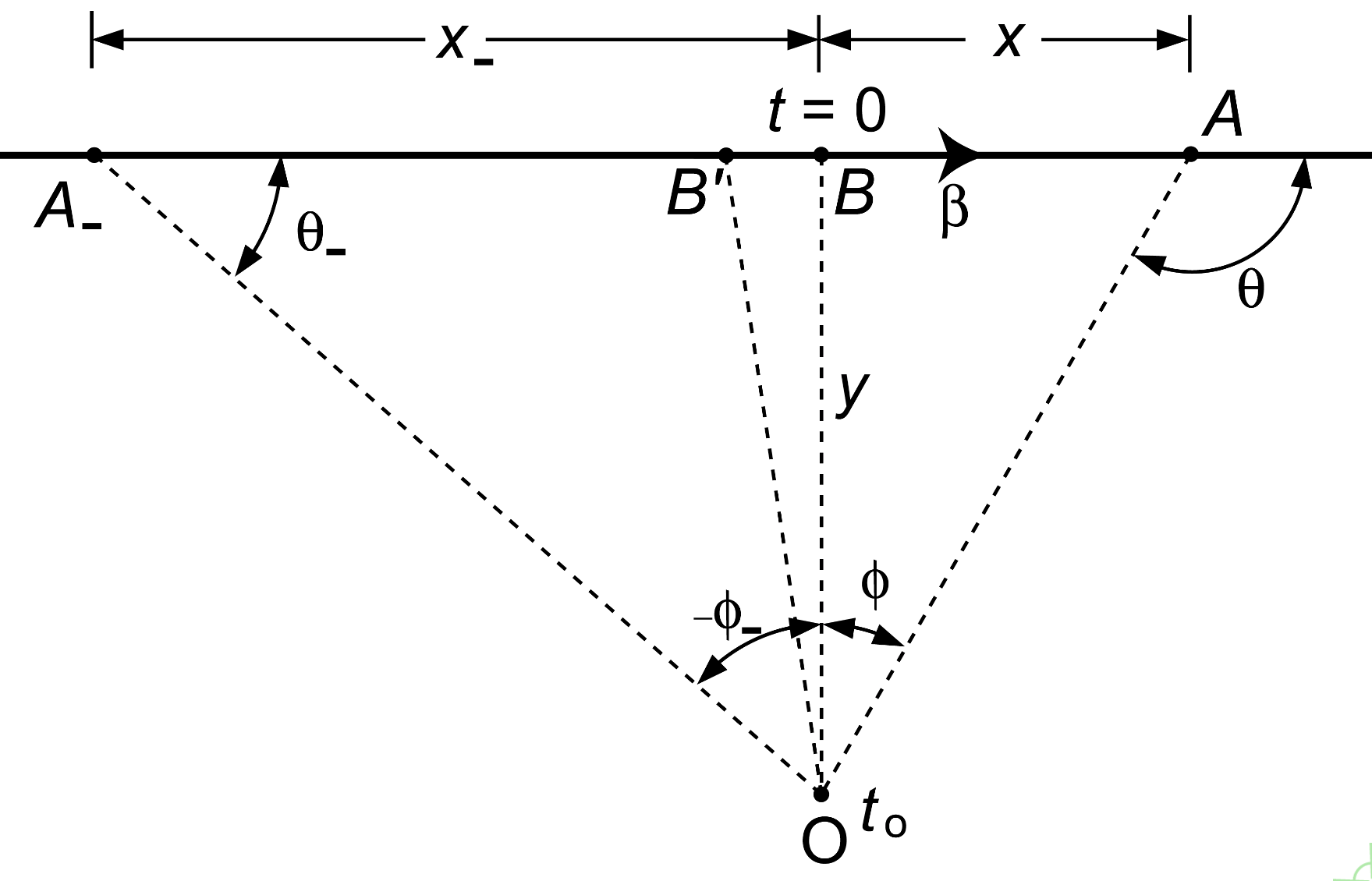
Here, the object is traveling along the thick horizontal line at a speed 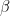 . The black dot in the animation (where the object first appears to the observer) is B’. B is the point of closest approach. Let’s set the time
. The black dot in the animation (where the object first appears to the observer) is B’. B is the point of closest approach. Let’s set the time 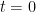 when the object is at the point B. The line of flight (at its closest point B) is at a distance of y from the observer at O. A is a typical point at a distance x from B.
when the object is at the point B. The line of flight (at its closest point B) is at a distance of y from the observer at O. A is a typical point at a distance x from B.  is the angle between the line of flight and the observer’s line of sight.
is the angle between the line of flight and the observer’s line of sight. 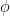 is that the angle that the object subtends at the observer’s position O with respect to the normal. Let’s set
is that the angle that the object subtends at the observer’s position O with respect to the normal. Let’s set  to simplify the algebra, so that
to simplify the algebra, so that 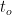 , the observer’s time is
, the observer’s time is  . (A- is another representative point where
. (A- is another representative point where  and
and 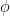 are negative.)
are negative.)
With these notations, we can write down the following equation for the real position of the object at time 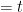 :
:
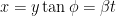
Or,
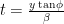
A photon emitted by the object at A (at time 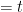 ) will reach O after traversing the hypotenuse. A photon emitted at B will reach the observer at
) will reach O after traversing the hypotenuse. A photon emitted at B will reach the observer at  , since we have chosen
, since we have chosen  . We have defined the observer’s time
. We have defined the observer’s time 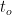 such that
such that  , then we have:
, then we have:
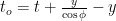
which gives the relation between 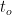 and
and 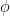 .
.

Expanding the equation for 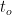 to second order, we get:
to second order, we get:

(Call this equation Q.)
The minimum value of 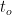 occurs at
occurs at 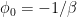 (which defines the position of the black dot in the animation, the point B’) and it is
(which defines the position of the black dot in the animation, the point B’) and it is 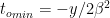 . To the observer, the object first appears at the position
. To the observer, the object first appears at the position 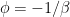 . Then it appears to stretch and split, rapidly at first, and slowing down later.
. Then it appears to stretch and split, rapidly at first, and slowing down later.
The quadratic equation Q above can be recast as:
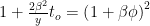
which will be more useful later in the derivation. (Call this equation U.)
The angular separation between the objects flying away from each other is the difference between the roots of the quadratic equation Q:



making use of the “useful” equation U above. Thus, we have the angular separation either in terms of the observer’s time (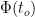 ) or the angular position of the object (
) or the angular position of the object ( ) as illustrated in the next figure, which illustrates how the angular separation is expressed either in terms of the observer’s time (
) as illustrated in the next figure, which illustrates how the angular separation is expressed either in terms of the observer’s time (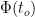 ) or the angular position of the object (
) or the angular position of the object ( ).
).
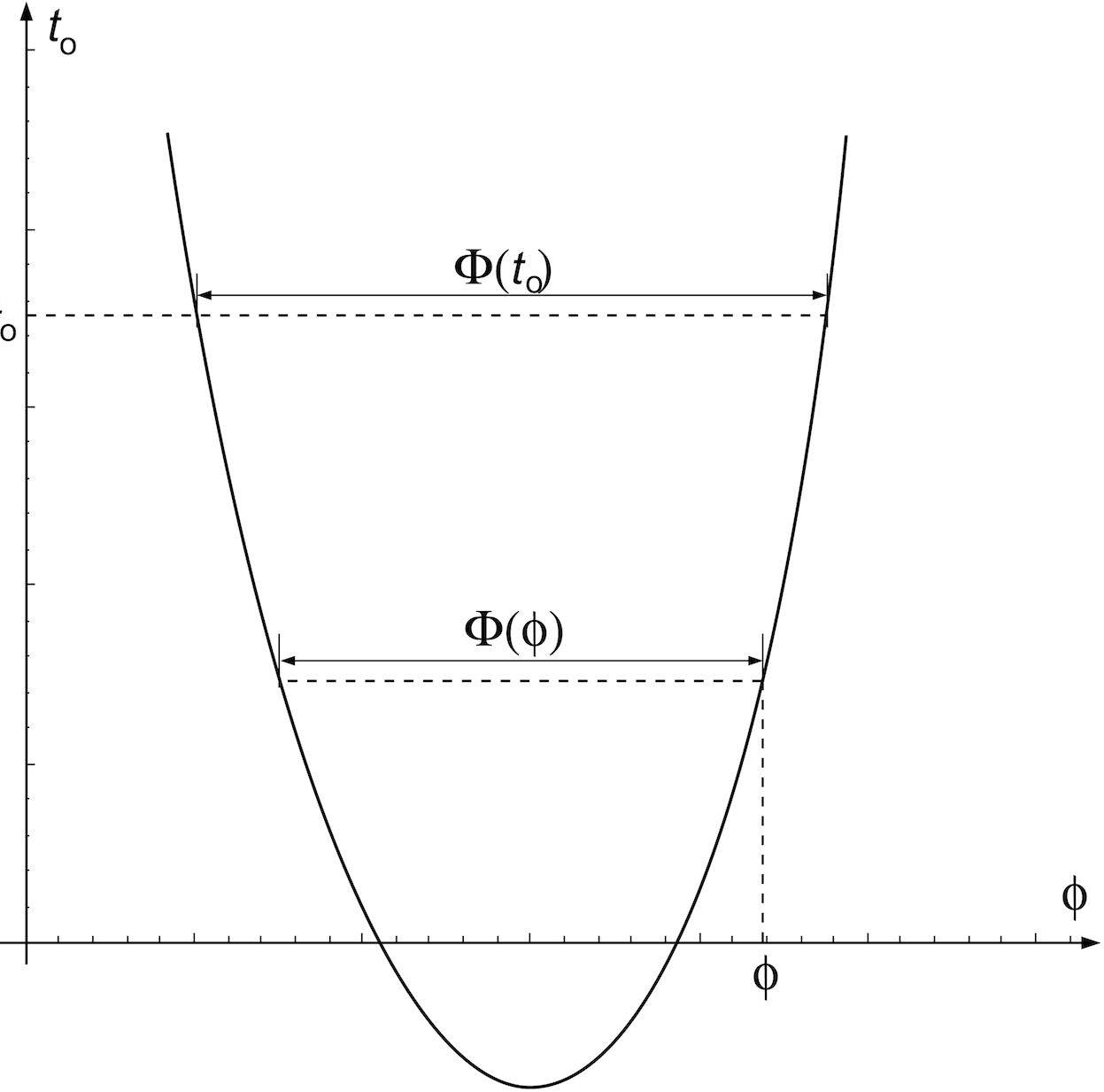
The rate at which the angular separation occurs is:
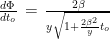
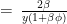
Again, making use of the useful equation U. Defining the apparent age of the formation  and knowing
and knowing 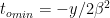 , we can write:
, we can write:

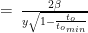
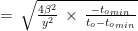

Note that in order to go from the angular rate to the speed (even the apparent speed), we need to estimate  , which is model-based.
, which is model-based.
Now, can you tell me why the object doesn’t appear at two places if 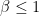 (subluminal object)? 🙂
(subluminal object)? 🙂
In fact, there is much more to this puzzle.
- The reason the dot on the right doesn’t move faster than c is closely related to way the relativistic speed limit is derived.
- One should also consider that saying that the dot is on the ceiling at a particular point at a certain instant of time is not good enough. When will the observer (presumably at the laser gun) see it? There is one more leg of light travel (from the dot back to the gun) that needs to included. This consideration may be behind the definition of simultaneity (using the round trip travel of light) in SR.
- To the left of the point of separation (the black point), the flow of time is reversed. In other words, if you changed the laser color as you scanned from the left edge of the figure to the center, the change in the color of the dot would appear in the reverse order (in time).
- The Doppler shift also is reversed in this region. This is why I was intrigued by the left-handed material, where the group velocity and the Doppler shift are reversed.