In the “Philosophical Implications” forum, there was an attempt to incorporate acceleration into Lorentz transformation using some clever calculus or numerical techniques. Such an attempt will not work because of a rather interesting geometric reason. I thought I would post the geometric interpretation of Lorentz transformation (or how to go from SR to GR) here.
Let me start with a couple of disclaimers. First of, what follows is my understanding of LT/SR/GR. I post it here with the honest belief that it is right. Although I have enough academic credentials to convince myself of my infallibility, who knows? People much smarter than me get proven wrong every day. And, if we had our way, we would prove even Einstein himself wrong right here in this forum, wouldn’t we? Secondly, what I write may be too elementary for some of the readers, perhaps even insultingly so. I request them to bear with it, considering that some other readers may find it illuminating. Thirdly, this post is not a commentary on the rightness or wrongness of the theories; it is merely a description of what the theories say. Or rather, my version of what they say. With those disclaimers out of the way, let’s get started…
LT is a rotation in the 4-D space-time. Since it not easy to visualize 4-D space-time rotation, let’s start with a 2-D, pure space rotation. One fundamental property of a geometry (such as 2-D Euclidean space) is its metric tensor. The metric tensor defines the inner product between two vectors in the space. In normal (Euclidean or flat) spaces, it also defines the distance between two points (or the length of a vector).
Though the metric tensor has the dreaded “tensor” word in its name, once you define a coordinate system, it is only a matrix. For Euclidean 2-D space with x and y coordinates, it is the identity matrix (two 1’s along the diagonal). Let’s call it G. The inner product between vectors A and B is A.B = Trans(A) G B, which works out to be 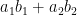 . Distance (or length of A) can be defined as
. Distance (or length of A) can be defined as 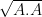 .
.
So far in the post, the metric tensor looks fairly useless, only because it is the identity matrix for Euclidean space. SR (or LT), on the other hand, uses Minkowski space, which has a metric that can be written with [-1, 1, 1, 1] along the diagonal with all other elements zero – assuming time t is the first component of the coordinate system. Let’s consider a 2-D Minkowski space for simplicity, with time (t) and distance (x) axes. (This is a bit of over-simplification because this space cannot handle circular motion, which is popular in some threads.) In units that make c = 1, you can easily see that the invariant distance using this metric tensor is 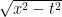 .
.

Comments are closed.