The uncertainty principle is the second thing in physics that has captured the public imagination. (The first one is 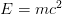 .) It says something seemingly straightforward — you can measure two complimentary properties of a system only to a certain precision. For instance, if you try to figure out where an electron is (measure its position, that is) more and more precisely, its speed becomes progressively more uncertain (or, the momentum measurement becomes imprecise).
.) It says something seemingly straightforward — you can measure two complimentary properties of a system only to a certain precision. For instance, if you try to figure out where an electron is (measure its position, that is) more and more precisely, its speed becomes progressively more uncertain (or, the momentum measurement becomes imprecise).
Where does this principle come from? Before we can ask that question, we have to examine what the principle really says. Here are a few possible interpretations:
- Position and momentum of a particle are intrinsically interconnected. As we measure the momentum more accurately, the particle kind of “spreads out,” as George Gamow’s character, Mr. Tompkins, puts it. In other words, it is just one of those things; the way the world works.
- When we measure the position, we disturb the momentum. Our measurement probes are “too fat,” as it were. As we increase the position accuracy (by shining light of shorter wavelengths, for instance), we disturb the momentum more and more (because shorter wavelength light has higher energy/momentum).
- Closely related to this interpretation is a view that the uncertainty principle is a perceptual limit.
- We can also think of the uncertainly principle as a cognitive limit if we consider that a future theory might surpass such limits.
All right, the last two interpretations are my own, so we won’t discuss them in detail here.
The first view is currently popular and is related to the so-called Copenhagen interpretation of quantum mechanics. It is kind of like the closed statements of Hinduism — “Such is the nature of the Absolute,” for instance. Accurate, may be. But of little practical use. Let’s ignore it for it is not too open to discussions.
The second interpretation is generally understood as an experimental difficulty. But if the notion of the experimental setup is expanded to include the inevitable human observer, we arrive at the third view of perceptual limitation. In this view, it is actually possible to “derive” the uncertainty principle.
Let’s assume that we are using a beam of light of wavelength 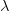 to observe the particle. The precision in the position we can hope to achieve is of the order of
to observe the particle. The precision in the position we can hope to achieve is of the order of 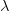 . In other words,
. In other words, 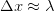 . In quantum mechanics, the momentum of each photon in the light beam is inversely proportional to the wavelength. At least one photon is reflected by the particle so that we can see it. So, by the classical conservation law, the momentum of the particle has to change by at least
. In quantum mechanics, the momentum of each photon in the light beam is inversely proportional to the wavelength. At least one photon is reflected by the particle so that we can see it. So, by the classical conservation law, the momentum of the particle has to change by at least 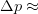 constant
constant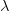 from what it was before the measurement. Thus, through perceptual arguments, we get something similar to the Heisenberg uncertainty principle
from what it was before the measurement. Thus, through perceptual arguments, we get something similar to the Heisenberg uncertainty principle 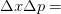 constant.
constant.
We can make this argument more rigorous, and get an estimate of the value of the constant. The resolution of a microscope is given by the empirical formula 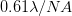 , where
, where 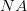 is the numerical aperture, which has a maximum value of one. Thus, the best spatial resolution is
is the numerical aperture, which has a maximum value of one. Thus, the best spatial resolution is 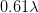 . Each photon in the light beam has a momentum
. Each photon in the light beam has a momentum 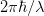 , which is the uncertainty in the particle momentum. So we get
, which is the uncertainty in the particle momentum. So we get 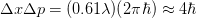 , approximately an order of magnitude bigger than the quantum mechanical limit. Through more rigorous statistical arguments, related to the spatial resolution and the expected momentum transferred, it may possible to derive the Heisenberg uncertainty principle through this line of reasoning.
, approximately an order of magnitude bigger than the quantum mechanical limit. Through more rigorous statistical arguments, related to the spatial resolution and the expected momentum transferred, it may possible to derive the Heisenberg uncertainty principle through this line of reasoning.
If we consider the philosophical view that our reality is a cognitive model of our perceptual stimuli (which is the only view that makes sense to me), my fourth interpretation of the uncertainty principle being a cognitive limitation also holds a bit of water.
Reference
The latter part of this post is an excerpt from my book, The Unreal Universe.


One thought on “Uncertainly Principle”
Comments are closed.