Whenever we talk about Quantum Mechanics, one of the first questions would be, “What about the cat?” This question, really, is about the interpretations of Quantum Mechanics. The standard interpretation, the so-called Copenhagen interpretation, leads to the famous Schrodinger’s cat.
Continue reading
Tag Archives: quantum mechanics
Quantum Field Theory
In this post on Quantum Mechanics (QM), we will go a bit beyond it and touch upon Quantum Field Theory – the way it is used in particle physics. In the last couple of posts, I outlined a philosophical introduction to QM, as well as its historical origin – how it came about as an ad-hoc explanation of the blackbody radiation, and a brilliant description of the photoelectric effect.
Continue reading
Historical Origin of Quantum Mechanics
In this section, we will try to look at the historical origin of Quantum Mechanics, which is usually presented succinctly using scary looking mathematical formulas. The role of mathematics in physics, as Richard Feynman explains (in his lectures on QED given in Auckland, New Zealand in 1979, available on YouTube, but as poor quality recordings) is purely utilitarian.
Continue reading
Quantum Mechanics
Quantum Mechanics (QM) is the physics of small things. How do they behave and how do they interact with each other? Conspicuously absent from this framework of QM is why. Why small things do what they do is a question QM leaves alone. And, if you are to make any headway into this subject, your best bet is to curb your urge to ask why. Nature is what she is. Our job is to understand the rules by which she plays the game of reality, and do our best to make use of those rules to our advantage in experiments and technologies. Ours is not to reason why. Really.
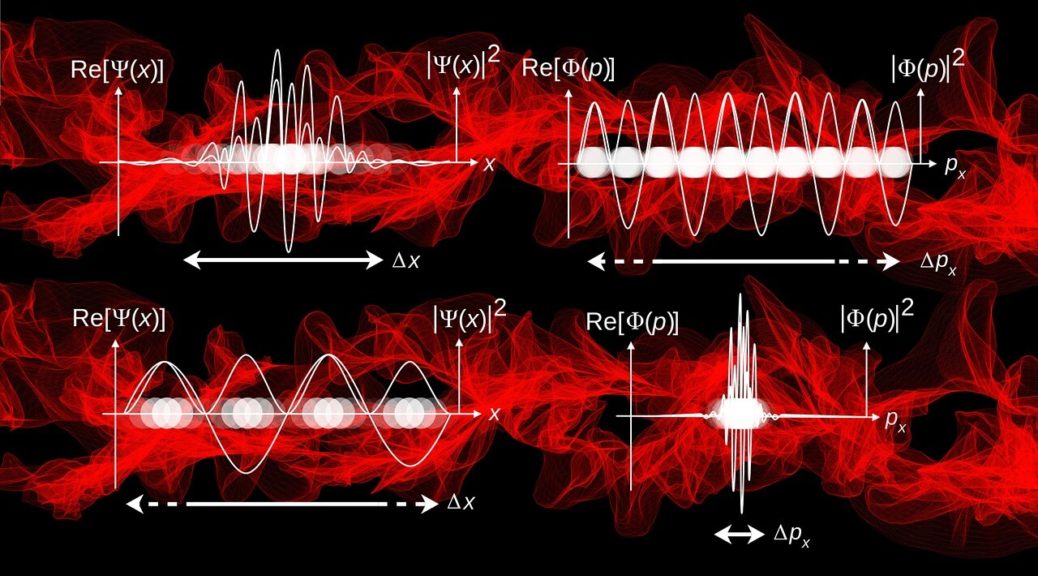
Uncertainly Principle
The uncertainty principle is the second thing in physics that has captured the public imagination. (The first one is  .) It says something seemingly straightforward — you can measure two complimentary properties of a system only to a certain precision. For instance, if you try to figure out where an electron is (measure its position, that is) more and more precisely, its speed becomes progressively more uncertain (or, the momentum measurement becomes imprecise).
.) It says something seemingly straightforward — you can measure two complimentary properties of a system only to a certain precision. For instance, if you try to figure out where an electron is (measure its position, that is) more and more precisely, its speed becomes progressively more uncertain (or, the momentum measurement becomes imprecise).
Where does this principle come from? Before we can ask that question, we have to examine what the principle really says. Here are a few possible interpretations:
- Position and momentum of a particle are intrinsically interconnected. As we measure the momentum more accurately, the particle kind of “spreads out,” as George Gamow’s character, Mr. Tompkins, puts it. In other words, it is just one of those things; the way the world works.
- When we measure the position, we disturb the momentum. Our measurement probes are “too fat,” as it were. As we increase the position accuracy (by shining light of shorter wavelengths, for instance), we disturb the momentum more and more (because shorter wavelength light has higher energy/momentum).
- Closely related to this interpretation is a view that the uncertainty principle is a perceptual limit.
- We can also think of the uncertainly principle as a cognitive limit if we consider that a future theory might surpass such limits.
All right, the last two interpretations are my own, so we won’t discuss them in detail here.
The first view is currently popular and is related to the so-called Copenhagen interpretation of quantum mechanics. It is kind of like the closed statements of Hinduism — “Such is the nature of the Absolute,” for instance. Accurate, may be. But of little practical use. Let’s ignore it for it is not too open to discussions.
The second interpretation is generally understood as an experimental difficulty. But if the notion of the experimental setup is expanded to include the inevitable human observer, we arrive at the third view of perceptual limitation. In this view, it is actually possible to “derive” the uncertainty principle.
Let’s assume that we are using a beam of light of wavelength 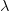 to observe the particle. The precision in the position we can hope to achieve is of the order of
to observe the particle. The precision in the position we can hope to achieve is of the order of 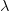 . In other words,
. In other words, 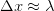 . In quantum mechanics, the momentum of each photon in the light beam is inversely proportional to the wavelength. At least one photon is reflected by the particle so that we can see it. So, by the classical conservation law, the momentum of the particle has to change by at least
. In quantum mechanics, the momentum of each photon in the light beam is inversely proportional to the wavelength. At least one photon is reflected by the particle so that we can see it. So, by the classical conservation law, the momentum of the particle has to change by at least 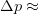 constant
constant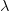 from what it was before the measurement. Thus, through perceptual arguments, we get something similar to the Heisenberg uncertainty principle
from what it was before the measurement. Thus, through perceptual arguments, we get something similar to the Heisenberg uncertainty principle 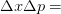 constant.
constant.
We can make this argument more rigorous, and get an estimate of the value of the constant. The resolution of a microscope is given by the empirical formula 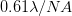 , where
, where 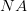 is the numerical aperture, which has a maximum value of one. Thus, the best spatial resolution is
is the numerical aperture, which has a maximum value of one. Thus, the best spatial resolution is 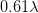 . Each photon in the light beam has a momentum
. Each photon in the light beam has a momentum 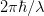 , which is the uncertainty in the particle momentum. So we get
, which is the uncertainty in the particle momentum. So we get 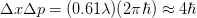 , approximately an order of magnitude bigger than the quantum mechanical limit. Through more rigorous statistical arguments, related to the spatial resolution and the expected momentum transferred, it may possible to derive the Heisenberg uncertainty principle through this line of reasoning.
, approximately an order of magnitude bigger than the quantum mechanical limit. Through more rigorous statistical arguments, related to the spatial resolution and the expected momentum transferred, it may possible to derive the Heisenberg uncertainty principle through this line of reasoning.
If we consider the philosophical view that our reality is a cognitive model of our perceptual stimuli (which is the only view that makes sense to me), my fourth interpretation of the uncertainty principle being a cognitive limitation also holds a bit of water.
Reference
The latter part of this post is an excerpt from my book, The Unreal Universe.
Sex and Physics — According to Feynman
Physics goes through an age of complacency once in a while. Complacency originates from a sense of completeness, a feeling that we have discovered everything there is to know, the path is clear and the methods well-understood.
Historically, these bouts of complacency are followed by rapid developments that revolutionize the way physics is done, showing us how wrong we have been. This humbling lesson of history is probably what prompted Feynman to say:
Such an age of complacency existed at the turn of the 19th century. Famous personas like Kelvin remarked that all that was left to do was to make more precise measurements. Michelson, who played a crucial role in the revolution to follow, was advised not to enter a “dead” field like physics.
Who would have thought that in less than a decade into the 20th century, we would complete change the way we think of space and time? Who in their right mind would say now that we will again change our notions of space and time? I do. Then again, nobody has ever accused me of a right mind!
Another revolution took place during the course of the last century — Quantum Mechanics, which did away with our notion of determinism and dealt a serious blow to the system-observer paradigm of physics. Similar revolutions will happen again. Let’s not hold on to our concepts as immutable; they are not. Let’s not think of our old masters as infallible, for they are not. As Feynman himself would point out, physics alone holds more examples of the fallibility of its old masters. And I feel that a complete revolution in thought is overdue now.
You might be wondering what all this has to do with sex. Well, I just thought sex would sell better. I was right, wasn’t I? I mean, you are still here!
Feynman also said,
Photo by “Caveman Chuck” Coker 
Einstein on God and Dice
Although Einstein is best known for his theories of relativity, he was also the main driving force behind the advent of quantum mechanics (QM). His early work in photo-voltaic effect paved way for future developments in QM. And he won the Nobel prize, not for the theories of relativity, but for this early work.
It then should come as a surprise to us that Einstein didn’t quite believe in QM. He spent the latter part of his career trying to device thought experiments that would prove that QM is inconsistent with what he believed to be the laws of nature. Why is it that Einstein could not accept QM? We will never know for sure, and my guess is probably as good as anybody else’s.
Einstein’s trouble with QM is summarized in this famous quote.
It is indeed difficult to reconcile the notions (or at least some interpretations) of QM with a word view in which a God has control over everything. In QM, observations are probabilistic in nature. That is to say, if we somehow manage to send two electrons (in the same state) down the same beam and observe them after a while, we may get two different observed properties.
We can interpret this imperfection in observation as our inability to set up identical initial states, or the lack of precision in our measurements. This interpretation gives rise to the so-called hidden variable theories — considered invalid for a variety of reasons. The interpretation currently popular is that uncertainty is an inherent property of nature — the so-called Copenhagen interpretation.
In the Copenhagen picture, particles have positions only when observed. At other times, they should be thought of as kind of spread out in space. In a double-slit interference experiment using electrons, for instance, we should not ask whether a particular electron takes on slit or the other. As long as there is interference, it kind of takes both.
The troubling thing for Einstein in this interpretation would be that even God would not be able to make the electron take one slit or the other (without disturbing the interference pattern, that is). And if God cannot place one tiny electron where He wants, how is he going to control the whole universe?