Everything in life comes at a cost — with a price tag seldom denominated in dollars and cents, and almost always hidden.
In our profession as quants and traders, we know we cannot accumulate if we don’t speculate (as P. G. Wodehouse puts it). So we accept and even welcome some of these price tags. We take certain risks, which we hope are calculated and understood, so that we can bring unto our employers what is theirs. These are good risks.
Bad risks are those we cannot understand and quantify, or measure and hedge against. They are bad because, even if we rake in some profits, we are never sure that they are commensurate with the downside we are throwing ourselves open to.
Market risk is a good risk. We know how to measure and model it, hedge against and reap rewards from it. We have smart people with bulging foreheads solving stochastic differential equations for us and simplifying the risk-reward equation.
Operational risk is a bad one. We can put as many software locks and control processes as we want around it. But we cannot prevent the rogue elements amongst us from sharing their passwords over a beer in some French brasserie. Worse, we have no idea what the rewards are when we expose ourselves to certain levels of operational risk. Heck, we don’t even know what the levels are because we have no means of quantifying it.
Incomplete appreciation of the risks involved in many situations is an almost philosophical factor that comes around to haunt us. It is not that we underestimate the risks; it is more like we are not aware of certain ramifications. The inconvenient warming of our home planet, for instance, is a consequence that the Wright brothers and Henry Ford simply could not have been aware of.
No such thing as a free lunch — the seemingly unlimited and practically free supply of nuclear energy has a not-so-hidden cost: the necessity to dispose of or securely store dangerous waste for, say, twenty thousand years. How do you store something for that long? After all, twenty thousand years ago, we were only barely human!
But the list of such boons and associated banes is endless. Think of the prosperity that a flattened world (using Thomas Friedman’s lingo) brought to emerging economies like India and China, which came at the expense of the cultural values that took thousands of years of careful nurturing.
A personal ramification of our high-powered corporate life is the alarming level of stress that we put ourselves through. Stress comes from market movements. As the sub-prime market tanked and heads started to roll, some of us had to worry about our heads. Fat bonuses of the first quarter usher in tax worries; lean bonuses indicate uncertain corporate future. Rogue traders burn billions and expose everybody to scrutiny and associated stresses. Even the lack of stress brings in some worries that the corporate world is perhaps passing us by!
When I first switched to the finance industry in late 2005, I happened to flip through an issue of the Bloomberg Market magazine. On of the first things struck me was that most of the advertisements seemed to be of expensive cars or alcohol. Is alcoholism the cost we readily dish out so that we can afford a gleaming dream machine?
Is stress a price worth paying for our corporate success? Are the risks worth their rewards?
Married to the Job — Till Death Do Us Part?
Stress is as much a part of our corporate careers as death is a fact of life. Still, it is best to keep the two (career and death) separate. This is the message that was lost on some hardworking young souls here in Singapore who literally worked themselves to death. So do a lot of Japanese, if we are to believe the media.
The reason for death in sedentary jobs is the insidious condition called deep vein thrombosis. This condition develops because of extended hours spent sitting, when a blood clot forms in the lower limbs. The clot then travels to the vital organs in the upper body, where it wreaks havoc including death.
The trick in avoiding such an untimely demise, of course, is not to sit for long. But that is easier said than done, when job pressure mounts, and deadlines loom.
Here is where you have to get your priorities straight. What do you value more? Quality of life or corporate success? The implication in this choice is that you can’t have both, as illustrated in the joke in investment banking that goes like: “If you can’t come in on Saturday, don’t bother coming in on Sunday!”
You can, however, make a compromise. It is possible to let go a little bit of career aspirations and improve the quality of life tremendously. This balancing act is not so simple though; nothing in life is.
Undermining work-life balance are a few factors. One is the materialistic culture we live in. It is hard to fight that trend. Second is a misguided notion that you can “make it” first, then sit back and enjoy life. That point in time when you are free from worldly worries rarely materializes. Thirdly, you may have a career-oriented partner. Even when you are ready to take a balanced approach, your partner may not be, thereby diminishing the value of putting it in practice.
These are factors you have to constantly battle against. And you can win the battle, with logic, discipline and determination. However, there is a fourth, much more sinister, factor, which is the myth that a successful career is an all-or-nothing proposition, as implied in the preceding investment banking joke. It is a myth (perhaps knowingly propagated by the bosses) that hangs over our corporate heads like the sword of Damocles.
Because of this myth, people end up working late, trying to make an impression. But an impression is made, not by the quantity of work, but by its quality. Turn in quality, impactful work, and you will be rewarded, regardless of how long it takes to accomplish it. Long hours, in my view, make the possibility of quality work remote.
Such melancholy long hours are best left to workaholics; they keep working because they cannot help it. It is not so much a career aspiration, but a force of habit coupled with a fear of social life.
To strike a work-life balance in today’s dog eat dog world, you may have to sacrifice a few upper rungs of the proverbial corporate ladder. Raging against the corporate machine with no regard to the consequences ultimately boils down to one simple realization — that making a living amounts to nothing if your life is lost in the process.
Spousal Indifference — Do We Give a Damn?
After a long day at work, you want to rest your exhausted mind; may be you want to gloat a bit about your little victories, or whine a bit about your little setbacks of the day. The ideal victim for this mental catharsis is your spouse. But the spouse, in today’s double income families, is also suffering from a tired mind at the end of the day.
The conversation between two tired minds usually lacks an essential ingredient — the listener. And a conversation without a listener is not much of a conversation at all. It is merely two monologues that will end up generating one more setback to whine about — spousal indifference.
Indifference is no small matter to scoff at. It is the opposite of love, if we are to believe Elie Weisel. So we do have to guard against indifference if we want to have a shot at happiness, for a loveless life is seldom a happy one.
“Where got time?” ask we Singaporeans, too busy to form a complete sentence. Ah… time! At the heart of all our worldly worries. We only have 24 hours of it in a day before tomorrow comes charging in, obliterating all our noble intensions of the day. And another cycle begins, another inexorable revolution of the big wheel, and the rat race goes on.
The trouble with the rat race is that, at the end of it, even if you win, you are still a rat!
How do we break this vicious cycle? We can start by listening rather than talking. Listening is not as easy as it sounds. We usually listen with a whole bunch of mental filters turned on, constantly judging and processing everything we hear. We label the incoming statements as important, useful, trivial, pathetic, etc. And we store them away with appropriate weights in our tired brain, ignoring one crucial fact — that the speaker’s labels may be, and often are, completely different.
Due to this potential mislabeling, what may be the most important victory or heartache of the day for your spouse or partner may accidentally get dragged and dropped into your mind’s recycle bin. Avoid this unintentional cruelty; turn off your filters and listen with your heart. As Wesley Snipes advises Woody Herrelson in White Men Can’t Jump, listen to her (or him, as the case may be.)
It pays to practice such an unbiased and unconditional listening style. It harmonizes your priorities with those your spouse and pulls you away from the abyss of spousal apathy. But it takes years of practice to develop the proper listening technique, and continued patience and deliberate effort to apply it.
“Where got time?” we may ask. Well, let’s make time, or make the best of what little time we got. Otherwise, when days add up to months and years, we may look back and wonder: Where is the life that we lost in living?
Stress and a Sense of Proportion
How can we manage stress, given that it is unavoidable in our corporate existence? Common tactics against stress include exercise, yoga, meditation, breathing techniques, reprioritizing family etc. To add to this list, I have my own secret weapons to battle stress that I would like to share with you. These weapons may be too potent; so use them with care.
One of my secret tactics is to develop a sense of proportion, harmless as it may sound. Proportion can be in terms of numbers. Let’s start with the number of individuals, for instance. Every morning, when we come to work, we see thousands of faces floating by, almost all going to their respective jobs. Take a moment to look at them — each with their own personal thoughts and cares, worries and stresses.
To each of them, the only real stress is their own. Once we know that, why would we hold our own stress any more important than anybody else’s? The appreciation of the sheer number of personal stresses all around us, if we stop to think about it, will put our worries in perspective.
Proportion in terms of our size also is something to ponder over. We occupy a tiny fraction of a large building that is our workplace. (Statistically speaking, the reader of this column is not likely to occupy a large corner office!) The building occupies a tiny fraction of the space that is our beloved city. All cities are so tiny that a dot on the world map is usually an overstatement of their size.
Our world, the earth, is a mere speck of dust a few miles from a fireball, if we think of the sun as a fireball of any conceivable size. The sun and its solar system are so tiny that if you were to put the picture of our galaxy as the wallpaper on your PC, they would be sharing a pixel with a few thousand local stars! And our galaxy — don’t get me started on that! We have countless billions of them. Our existence (with all our worries and stresses) is almost incomprehensibly small.
The insignificance of our existence is not limited to space; it extends to time as well. Time is tricky when it comes to a sense of proportion. Let’s think of the universe as 45 years old. How long do you think our existence is in that scale? Eight seconds if we are very lucky!
We are created out of star dust, last for a mere cosmological instant, and then turn back into star dust. DNA machines during this time, we run unknown genetic algorithms, which we mistake for our aspirations and achievements, or stresses and frustrations. Relax! Don’t worry, be happy!
Sure, you may get reprimanded if that report doesn’t go out tomorrow. Or, your trader may bite your head off if that pricing model is delayed again. Or, your colleague may send out that backstabbing email (and Bcc your boss) if you displease them. But, don’t you get it, in this mind-numbingly humongous universe, it doesn’t matter an iota. In the big scheme of things, your stress is not even static noise!
Arguments for maintaining a level of stress all hinge on an ill-conceived notion that stress aids productivity. It does not. The key to productivity is an attitude of joy at work. When you stop worrying about reprimands and backstabs and accolades, and start enjoying what you do, productivity just happens. I know it sounds a bit idealistic, but my most productive pieces of work happened that way. Enjoying what I do is an ideal I will shoot for any day.
Stress and Metaphysics
Realizing that our existence is a mere blink of an eye in time, and less than a speck of dust in space is a powerful way of cutting our stress to size. My favorite weapon, however, is even more potent. I ask myself a basic question — what are space and time to begin with?
These may sound like silly metaphysical musings that have no relevance to real life. But they have been the subject matter of many lifelong quests over the ages. If we, humanity as a whole, cannot stop pondering over such things, it is probably because they form the basis of our existence. Besides, our stress takes place in space and time.
Philosophical grand-standing aside, let’s get to the meat of the problem: What is space? Space seems to be closely associated with our sense of sight. It also forms the basis of our reality — everything happens in space and time. For this reason, “What are space and time?” is a question that cannot be reduced to simpler elements in our reality.
We can, however, approach the issue by posing a similar question “What is sound?” Sound is an experience associated with hearing, clearly. But what is it? The answer is hinted at in the age-old conundrum of a falling tree in a deserted forest. Does it make sound? A popular topic of conservation in cocktail parties, this question is also a serious contemplative inquiry for a Zen monk.
The knee-jerk response to the question is, yes, the tree does make sound. It’s just that there is nobody to hear it. But hear what exactly?
Sure, the falling tree creates air pressure waves. But, the waves are not sound. These waves create an electrical signal in the ear, if an ear is present. Electrical signals are electrical signals, not sound. These signals, when transported to the brain, induce neuronal firing, which is still not sound. It is a fallacy to think of sound as anything physical, anything real. Sound is an experience or a cognitive representation associated with the input signals (which are the pressure waves, we think. But are they?)
We can draw similar analogies between other sensations and the corresponding signals — taste and smell to chemical composition, for instance. What about sight? What is the “sensation” or the cognitive representation associated with sight? It is what we think of as space.
Of course, we think of space as real, as the basis of our reality. It takes more than this short column to shake our belief in it. That’s why I wrote my book — The Unreal Universe.
To me, the unreal nature of what we consider reality is more than a constant contemplation. It is a source of a Zen-like immunity against stress and other worldly worries.
Yes, stress is the cost exacted by the corporate chain of command. It is a cost most of us happily pay, for the rewards are abundantly clear. But we have to be aware of the risks associated with the rewards — both in accepting them and in declining them.






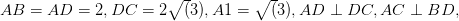 and foot of perpendicular is
and foot of perpendicular is 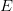 ,
,
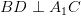
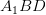 and
and 
 and
and  which are in different planes.
which are in different planes.
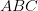 is a right angle,
is a right angle, 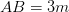
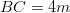
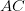 ?
?