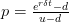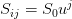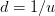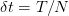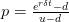Mathematical finance is built on a couple of assumptions. The most fundamental of them is the one on market efficiency. It states that the market prices every asset fairly, and the prices contain all the information available in the market. In other words, you cannot glean any more information by doing any research or technical analysis, or indeed any modeling. If this assumption doesn’t pan out, then the quant edifice we build on top of it will crumble. Some may even say that it did crumble in 2008.
We know that this assumption is not quite right. If it was, there wouldn’t be any transient arbitrage opportunities. But even at a more fundamental level, the assumption has shaky justification. The reason that the market is efficient is that the practitioners take advantage of every little arbitrage opportunity. In other words, the markets are efficient because they are not so efficient at some transient level.
Mark Joshi, in his well-respected book, “The Concepts and Practice of Mathematical Finance,” points out that Warren Buffet made a bundle of money by refusing to accept the assumption of market efficiency. In fact, the weak form of market efficiency comes about because there are thousands of Buffet wannabes who keep their eyes glued to the ticker tapes, waiting for that elusive mispricing to show up.
Given that the quant careers, and literally trillions of dollars, are built on the strength of this assumption, we have to ask this fundamental question. Is it wise to trust this assumption? Are there limits to it?
Let’s take an analogy from physics. I have this glass of water on my desk now. Still water, in the absence of any turbulence, has a flat surface. We all know why – gravity and surface tension and all that. But we also know that the molecules in water are in random motion, in accordance with the same Brownian process that we readily adopted in our quant world. One possible random configuration is that half the molecules move, say, to the left, and the other half to the right (so that the net momentum is zero).
If that happens, the glass on my desk will break and it will make a terrible mess. But we haven’t heard of such spontaneous messes (from someone other than our kids, that is.)
The question then is, can we accept the assumption on the predictability of the surface of water although we know that the underlying motion is irregular and random? (I am trying to make a rather contrived analogy to the assumption on market efficiency despite the transient irregularities.) The answer is a definite yes. Of course, we take the flatness of liquid surfaces for granted in everything from the useless lift-pumps and siphons of our grade school physics books all the way to dams and hydro-electric projects.
So what am I quibbling about? Why do I harp on the possibility of uncertain foundations? I have two reasons. One is the question of scale. In our example of surface flatness vs. random motion, we looked at a very large collection, where, through the central limit theorem and statistical mechanics, we expect nothing but regular behavior. If I was studying, for instance, how an individual virus propagates through the blood stream, I shouldn’t make any assumptions on the regularity in the behavior of water molecules. This matter of scale applies to quantitative finance as well. Are we operating at the right scale to ignore the shakiness of the market efficiency assumption?
The second reason for mistrusting the pricing models is a far more insidious one. Let me see if I can present it rather dramatically using my example of the tumbler of water. Suppose we make a model for the flatness of the water surface, and the tiny ripples on it as perturbations or something. Then we proceed to use this model to extract tiny amounts of energy from the ripples.
The fact that we are using the model impacts the flatness or the nature of the ripples, affecting the underlying assumptions of the model. Now, imagine that a large number of people are using the same model to extract as much energy as they can from this glass of water. My hunch is that it will create large scale oscillations, perhaps generating configurations that do indeed break the glass and make a mess. Discounting the fact that this hunch has its root more in the financial mess that spontaneously materialized rather than any solid physics argument, we can still see that large fluctuations do indeed seem to increase the energy that can be extracted. Similarly, large fluctuations (and the black swans) may indeed be a side effect of modeling.

 and
and 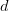 during a small time interval
during a small time interval 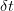 . Stringing together many such time intervals, we make up the expiration time of the derivative instrument we are trying to price. The derivative defined as a function of the price of the underlying at any point in time.
. Stringing together many such time intervals, we make up the expiration time of the derivative instrument we are trying to price. The derivative defined as a function of the price of the underlying at any point in time.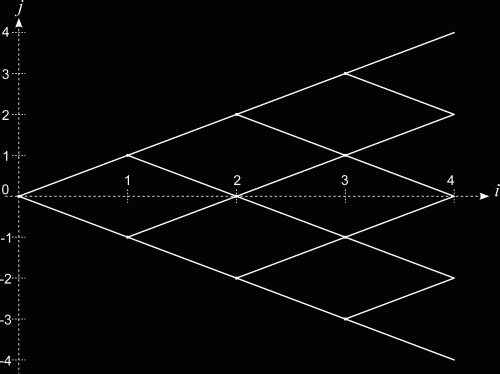
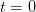 , we have the asset price
, we have the asset price 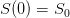 . At
. At 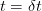 (with the maturity
(with the maturity 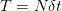 ). we have two possible asset values
). we have two possible asset values 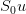 and
and 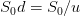 , where we have chosen
, where we have chosen 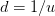 . In general, at time
. In general, at time 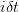 , at the asset price node level
, at the asset price node level 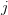 , we have
, we have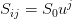
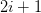 price nodes at any time step
price nodes at any time step 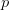 . With these notations, we can write down the fair value of an American call option (of expiry
. With these notations, we can write down the fair value of an American call option (of expiry 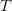 , underlying asset price
, underlying asset price 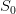 , strike price
, strike price 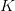 , risk free interest rate
, risk free interest rate  , asset price volatility
, asset price volatility 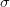 and number of time steps in the binomial tree
and number of time steps in the binomial tree 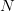 ) using the binomial tree pricing model as follows:
) using the binomial tree pricing model as follows: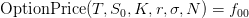
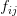 denotes the fair value of the option at any the node
denotes the fair value of the option at any the node 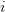 in time and
in time and 
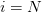 and
and 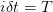 , where we exercise the option if it is in the money, which is what the first Max function denotes. The last term in the express above represents the risk neutral backward propagation of the option price from the time layer at
, where we exercise the option if it is in the money, which is what the first Max function denotes. The last term in the express above represents the risk neutral backward propagation of the option price from the time layer at 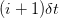 to
to 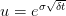 and the downward movement is chosen to be the same
and the downward movement is chosen to be the same